题目内容
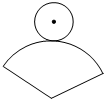 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若扇形的半径为4,圆心角为90°,则圆的半径为
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若扇形的半径为4,圆心角为90°,则圆的半径为1
1
.分析:利用圆锥的底面周长等于侧面展开图的扇形弧长,根据弧长公式计算.
解答:解:扇形的弧长是:
=2π,
设圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:2π=2πr,
则r=1,
故答案为:1.
| 90π×4 |
| 180 |
设圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:2π=2πr,
则r=1,
故答案为:1.
点评:本题考查了有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
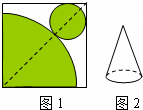 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )| A、R=2r | ||
B、R=
| ||
| C、R=3r | ||
| D、R=4r |
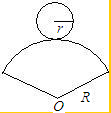 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的半径为R,且扇形的圆心角为120°,则r与R之间的关系是R=
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的半径为R,且扇形的圆心角为120°,则r与R之间的关系是R= (2013•宁波模拟)如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( )
(2013•宁波模拟)如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为( ) 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若该圆的半径为1,扇形的圆心角等于60°,则这个扇形的半径R的值是
如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若该圆的半径为1,扇形的圆心角等于60°,则这个扇形的半径R的值是