题目内容
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心,
AC长为半径作⊙O,交B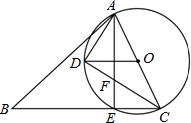 C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
(1)求证:D是
的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若
=
,且AC=4,求CF的长.
| 1 |
| 2 |
 C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
C于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.(1)求证:D是
 |
| AE |
(2)求证:∠DAO=∠B+∠BAD;
(3)若
| S△CEF |
| S△OCD |
| 1 |
| 2 |
分析:(1)判断出OD⊥AE,则利用垂径定理可得出点D是
的中点;
(2)延长AD交BC于H,利用外角可得出∠AHC=∠B+∠BAD,再由OA=OD,可得出结论.
(3)根据OA=OC可得出△OCD和△ACD的面积比,从而结合
=
可得出△CEF和△ACD的面积比,判断出△ACD∽△FCE,利用面积比等于相似比的平方即可解出CF的值.
 |
| AE |
(2)延长AD交BC于H,利用外角可得出∠AHC=∠B+∠BAD,再由OA=OD,可得出结论.
(3)根据OA=OC可得出△OCD和△ACD的面积比,从而结合
| S△CEF |
| S△OCD |
| 1 |
| 2 |
解答:证明:(1)∵AC是⊙O的直径,
∴AE⊥BC,
∵OD∥BC
∴AE⊥OD,
∴D是
的中点(垂径定理).
(2)如图,延长AD交BC于H,
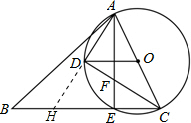
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAO=∠B+∠BAD.
(3)∵AO=OC,
∴S△OCD=
S△ACD,
∵
=
,
∴
=
,
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴
=(
)2,即:
=(
)2,
∴CF=2.
∴AE⊥BC,
∵OD∥BC
∴AE⊥OD,
∴D是
 |
| AE |
(2)如图,延长AD交BC于H,

则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠ADO=∠DAO,
∴∠DAO=∠B+∠BAD.
(3)∵AO=OC,
∴S△OCD=
| 1 |
| 2 |
∵
| S△CEF |
| S△OCD |
| 1 |
| 2 |
∴
| S△CEF |
| S△ACD |
| 1 |
| 4 |
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴
| S△CEF |
| S△ACD |
| CF |
| AC |
| 1 |
| 4 |
| CF |
| 4 |
∴CF=2.
点评:此题属于圆的综合题,涉及了垂径定理、三角形的外角、相似三角形的判定与性质,要求我们掌握底边在一条直线上且高相等的三角形的面积之比等于底边之比,相似三角形的面积之比等于相似比的平方,难度较大.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
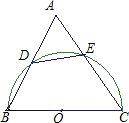 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
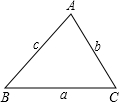 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: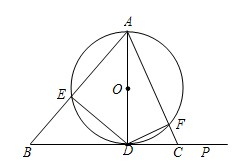 25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.
25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.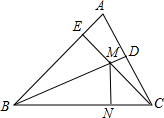 如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=
如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=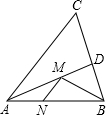 如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是
如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是