题目内容
如图，在Rt△ABC中，∠C＝90°，∠A＝30°，E为AB上一点，且AE：EB＝4：1，EF⊥AC于F，连结FB，则tan∠CFB的值等于
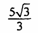
设BC=x，易得AC=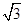
x，进而根据平行线的性质，可得FC=
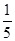AC=
．
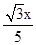在Rt△BFC中，根据三角函数的定义计算．
解：设BC=x，∵∠A=30°，∴AC=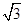x．
又∵AE：EB=4：1，EF∥BC，
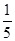∴FC=AC=．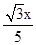
在Rt△BFC中，
tan∠CFB=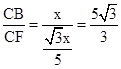
．
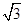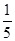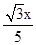x，进而根据平行线的性质，可得FC=AC=．在Rt△BFC中，根据三角函数的定义计算．
解：设BC=x，∵∠A=30°，∴AC=
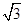x．又∵AE：EB=4：1，EF∥BC，
∴FC=
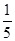AC=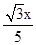．在Rt△BFC中，
tan∠CFB=
．
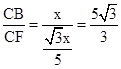练习册系列答案
相关题目
角的方向飞行，飞行到中途，再沿与原来的飞行方向成450角的方向继续飞行直到终
点。这样飞机的飞行路程比原来的路程控交换机600km远了多少？
.
礁的危险？ （参考数据：
）
）米
中，
，
，求
的长．