题目内容
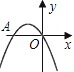
【题目】如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0) , 且x1+x2=4, ![]() .
.

(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.
【答案】(1)该抛物线的代数表达式为y=-x2+4x-3;(2)直线BC的代数表达式为y=x-3;(3)S△ABC=3.
【解析】试题分析:(1)先解方程组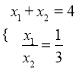 , 求得x1、x2的值,再代入抛物线y=-x2+bx+c即可求得抛物线的代数表达式;
, 求得x1、x2的值,再代入抛物线y=-x2+bx+c即可求得抛物线的代数表达式;
(2)设直线BC的表达式为y=kx+m,先求得抛物线与y轴的交点坐标,再根据待定系数法即可求得直线BC的表达式;
(3)分别求出AB、OC的长,再根据三角形的面积公式即可求得结果.
(1)解方程组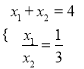 , 得x1=1,x2=3.
, 得x1=1,x2=3.
故![]() ,解这个方程组,得b=4,c=-3.
,解这个方程组,得b=4,c=-3.
所以,该抛物线的代数表达式为y=-x2+4x-3.
(2)设直线BC的表达式为y=kx+m.
由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).
所以![]() ,解得
,解得![]()
∴直线BC的代数表达式为y=x-3
(3)由于AB=3-1=2,OC=│-3│=3.
故S△ABC=![]() AB·OC=
AB·OC=![]() ×2×3=3.
×2×3=3.

练习册系列答案
相关题目