题目内容
【题目】如图,在直角△ABC中,∠C=90°,DE垂直平分AB,交BC于点D、交AB于点E.
(1)若AD平分∠CAB,则∠B的度数是 度;
(2)若AB=10,△ACD的周长为14,求△ACB的周长.
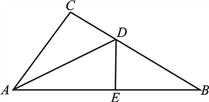
【答案】(1)∠B的度数是 30 度;(2)△ACB的周长24.
【解析】试题分析:(1)根据线段垂直平分线得出AD=BD,推出∠B=∠DAB,求出∠CAD=∠DAB=∠B,根据三角形内角和定理得出3∠B=90°,求出即可;
(2)根据△ACD的周长和AD=BD推出AC+BC=14,即可求出△ACB周长.
试题解析:解:(1)∵DE垂直平分AB,∴AD=BD,∴∠B=∠DAB,∵∠CAB的平分线AD,∴∠CAD=∠DAB=∠B,∵∠C=90°,∴3∠B=90°,∴∠B=30°;
(2)∵△ACD的周长14,∴AC+CD+AD=14,∵AD=BD,∴AC+CD+BD=AC+BC=14,∵AB=10,∴△ACB的周长是AC+BC+AB=24.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目