题目内容
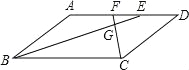
【题目】如图,在ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
A.2![]() B.4 C.4
B.4 C.4![]() D.5
D.5
【答案】C.
【解析】
试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=![]() ∠ABC+
∠ABC+![]() ∠DCB=90°
∠DCB=90°
∴EB⊥FC;
过A作AM∥FC,交BC于M,如图所示:
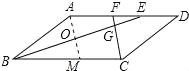
∵AM∥FC,
∴∠AOB=∠FGB,
∵EB⊥FC,
∴∠FGB=90°,
∴∠AOB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中,
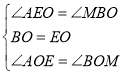 ,
,
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=2,
∴AO=1,
∴EO=![]() ,
,
∴BE=4![]()
故选C.

练习册系列答案
相关题目