题目内容
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0,解答下列问题: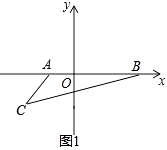
(1)填空:a= , b=;
(2)如图1,在第三象限内有一点C(﹣2,m),请用含m的式子表示△ABC的面积;
(3)在(2)的条件下,当m=﹣ ![]() 时,如图2,过点C作CD⊥y轴,交y轴于点D,在CD的延长线上有一动点P,连结BP,当四边形ODPB的面积与△ABC的面积相等,请求出点P的坐标.
时,如图2,过点C作CD⊥y轴,交y轴于点D,在CD的延长线上有一动点P,连结BP,当四边形ODPB的面积与△ABC的面积相等,请求出点P的坐标.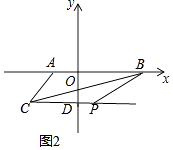
【答案】
(1)﹣1,3
(2)解:如图1,过C作CE⊥x轴于E,
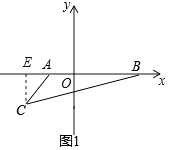
∵A(﹣1,0),B(3,0),
∴AB=4,
∵在第三象限内有一点C(﹣2,m),
∴CE=|m|=﹣m,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×4×(﹣m)=﹣2m;
×4×(﹣m)=﹣2m;
(3)解:当m=﹣ ![]() 时,
时,
∴S△ABC=3,
设P(n,﹣ ![]() ),
),
则四边形ODPB= ![]() ×
× ![]() (n+3)=
(n+3)= ![]() n+
n+ ![]() ,
,
∵四边形ODPB的面积与△ABC的面积相等,
∴ ![]() n+
n+ ![]() =3,
=3,
∴n=1,
∴点P的坐标(1,﹣ ![]() ).
).
【解析】【答案】解:(1)∵|a+1|+(b-3)2=0,
∴a+1=0,b-3=0,
∴a=-1,b=3;
(2)如图1,过C作CE⊥x轴于E,

∵A(﹣1,0),B(3,0),
∴AB=4,
∵在第三象限内有一点C(﹣2,m),
∴CE=|m|=﹣m,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×4×(﹣m)=﹣2m;
×4×(﹣m)=﹣2m;
(3)当m=﹣ 3 2 时,
∴S△ABC=3,
设P(n,﹣ ![]() ),
),
则四边形ODPB= ![]() ×
× ![]() (n+3)=
(n+3)= ![]() n+
n+ ![]() ,
,
∵四边形ODPB的面积与△ABC的面积相等,
∴ ![]() n+
n+ ![]() =3,
=3,
∴n=1,
∴点P的坐标(1,﹣ ![]() ).
).
所以案是:(1)-1,3;(2)﹣2m;(3)(1,﹣![]() ).
).
(1)根据非负数的性质即可得到结论;
(2)如图1,过C作CE⊥x轴于E,根据三角形的面积公式即可得到结论;
(3)当m=-![]() 时,得到S△ABC=3,设P(n,-
时,得到S△ABC=3,设P(n,-![]() ),根据四边形ODPB的面积与△ABC的面积相等,列方程即可得到结论.
),根据四边形ODPB的面积与△ABC的面积相等,列方程即可得到结论.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③