题目内容
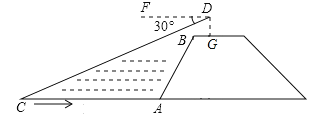
【题目】如图1是一张长方形的纸带,将这张纸带沿EF折叠成图2,再沿BF折叠成图3.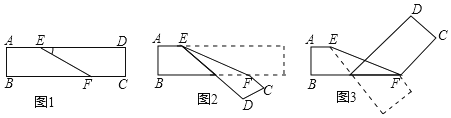
(1)若∠DEF=20°,请你求出图3中∠CFE度数;
(2)若∠DEF=a,请你直接用含a的式子表示图3中∠CFE的度数.
【答案】
(1)解:∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣20°=160°,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=20°,
∴图2中,∠BFC=160°﹣20°=140°,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+20°=140°,
∴图3中,∠CFE=120°
(2)解: 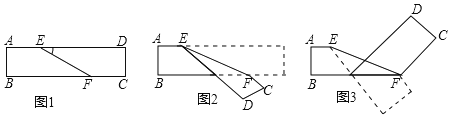
∵矩形对边AD∥BC,
∴CF∥DE,
∴图1中,∠CFE=180°﹣∠DEF=180°﹣a,
∵矩形对边AD∥BC,
∴∠BFE=∠DEF=a,
∴图2中,∠BFC=180°﹣2a,
由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,
∴图3中,∠CFE+a=180°﹣2a,
∴图3中,∠CFE=180°﹣3a.
【解析】根据矩形的性质可解.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.

练习册系列答案
相关题目