��Ŀ����
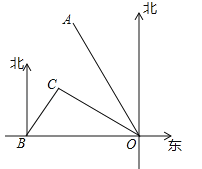
����Ŀ����ͼ��ʾ���ۿ�Bλ�ڸۿ�O��������120km����С��Cλ�ڸۿ�O��ƫ��60��ķ���һ���δ��Ӹۿ�O��������OA����ƫ��30�㣩��vkm/h���ٶ�ʻ��ۿ�O��ͬʱһ�ҿ�ͧ�Ӹۿ�B�������ر�ƫ��30��ķ�����60km/h���ٶ�ʻ��С��C����С��C��1h��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��
��1����ͧ�Ӹۿ�B��С��C��Ҫ�ʱ�䣿
��2������ͧ��С��C�����δ�����ǡ����ʱ1h����v��ֵ����������ۿ�O�ľ��룮
���𰸡���1��1����2��v=20km/h��OE=60km��v=40km/h��OE=120km��
��������
�����������1��Ҫ��B��C��ʱ�䣬��֪���ٶȣ���ֻҪ���BC��·�̣�������·�̹�ʽ������������ʱ�䣻
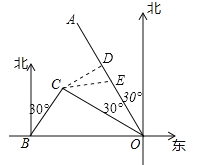
��2����C��CD��OA������ΪD������ᴦΪ��E�����OC=OBcos30��=![]() ��CD=
��CD=![]() OC=
OC=![]() ��OD=OCcos30��=90����DE=90��3v����ֱ����CDE�����ù��ɶ����ó�
��OD=OCcos30��=90����DE=90��3v����ֱ����CDE�����ù��ɶ����ó�![]() ����
����![]() ���ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
���ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
�����������1���ߡ�CBO=60�㣬��COB=30�㣬���BCO=90�㣮��Rt��BCO�У���OB=120����BC=![]() OB=60������ͧ�Ӹۿ�B��С��C��ʱ��Ϊ��60��60=1��Сʱ����
OB=60������ͧ�Ӹۿ�B��С��C��ʱ��Ϊ��60��60=1��Сʱ����
��2����C��CD��OA������ΪD������ᴦΪ��E����OC=OBcos30��=![]() ��CD=
��CD=![]() OC=
OC=![]() ��OD=OCcos30��=90����DE=90��3v����CE=60��
��OD=OCcos30��=90����DE=90��3v����CE=60��![]() ����
����![]() ����v=20��40������v=20km/hʱ��OE=3��20=60km����v=40km/hʱ��OE=3��40=120km��
����v=20��40������v=20km/hʱ��OE=3��20=60km����v=40km/hʱ��OE=3��40=120km��

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�����Ŀ���̳�����A��B������Ʒ�����ǵĽ��ۺ��ۼ������ʾ��
A��Ʒ | B��Ʒ | |
���ۣ�Ԫ/���� | 30 | 40 |
�ۼۣ�Ԫ/���� | 50 | 70 |
��1�������̳�����A��B������Ʒ��60����ǡ����ȥ2050Ԫ����A��B������Ʒ�����ټ���
��2�����̳��ڶ��ι���A��B������Ʒ����B��Ʒ������A��Ʒ������2����6�����ҹ����ܶ����2840Ԫ������������1900Ԫ������������̳������Ӧ�Ľ���������
��3����һ�����ڸ��̳�����A��B������Ʒ��������ǡ����140Ԫ��������A��B������Ʒ�����ټ���