题目内容
21、已知函数y=kx+5与函数y=8x-2k的交点的横坐标为x=1，求这两个函数的解析式．
分析：把x=1代入两个函数关系式，根据函数值相等，列方程求k的值．
解答：解：因为x=1是y=kx+5与y=8x-2k交点的横坐标，
所以当x=1时，它们的纵坐标相等，
即：k+5=8-2k，
解得：k=1，
所以当x=1时，两个函数表达式分别是：y=x+5，y=8x-2．
所以当x=1时，它们的纵坐标相等，
即：k+5=8-2k，
解得：k=1，
所以当x=1时，两个函数表达式分别是：y=x+5，y=8x-2．
点评：用待定系数法确定函数的解析式，是常用的一种解题方法．
练习册系列答案
名校课堂系列答案
相关题目
已知函数y=
(k＞0)，当k取不同的数值时，可以得到许多不同的双曲线，这些双曲线必定（ ）
| k |
| x |
| A、交于同一个交点 |
| B、有无数个交点 |
| C、没有交点 |
| D、不能确定 |
已知函数y=
，当x=1时，y=-3，那么这个函数的解析式是（ ）
| k |
| x |
A、y=
| ||
B、y=
| ||
| C、y=3x | ||
| D、y=-3x |
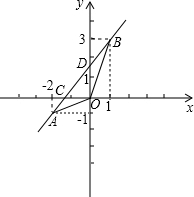已知函数y=kx+b的图象经过A（-2，-1）、B（1，3）两点，分别交x、y轴于点C、D．