题目内容
在平面直角坐标系中，△ABC三个顶点的坐标分别是A（3，6）、B（1，4）、C（1，0）．
（1）△ABC外接圆的圆心坐标是________；
（2）求以BC为轴，将△ABC旋转一周所得几何体的全面积（即求所有表面的面积之和，结果保留根号和π）
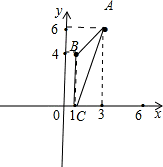解：（1）（5，2）；（2）旋转后得到的几何体是一个以2为底面半径、6为高的大圆锥，再挖掉一个以2为底面圆的半径、2为高的小圆锥．
它们的母线之长分别为AC=
；AB=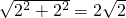
所求全面积为：
．分析：（1）可先设圆心坐标为（x，y），再根据“三角形外接圆的圆心到三角形三顶点的距离相等”列出等式，化简即可得出圆心的坐标
（2）根据题意得到三角形ABC选转一周所得的几何体为圆锥，利用圆锥的表面积的计算方法求得其表面积即可．
点评：本题考查了圆锥的计算，解题的关键是牢记圆锥的有关公式．
练习册系列答案
相关题目
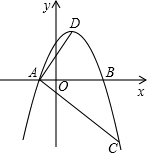坐标原点．A、B两点的横坐标分别是方程x2-4x-12=0的两根，且cos∠DAB=
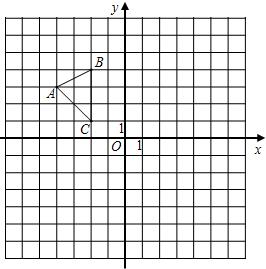18、在平面直角坐标系中，把一个图形先绕着原点顺时针旋转的角度为θ，再以原点为位似中心，相似比为k得到一个新的图形，我们把这个过程记为【θ，k】变换．例如，把图中的△ABC先绕着原点O顺时针旋转的角度为90°，再以原点为位似中心，相似比为2得到一个新的图形△A1B1C1，可以把这个过程记为【90°，2】变换．