题目内容
 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.(1)求证:AD=BE;
(2)求证:MN∥AE;
(3)若点C在AE上运动(点C不与A、E重合),当点C运动到什么位置时,线段MN的长度最大?最大值是多少?
分析:(1)由条件可以得出BC=AC,DC=EC,∠ACB=∠DCE=60°,可以得出∠ACD=∠BCE,就可以△ACD≌△BCE,从而可以得出结论.
(2)由△ACD≌△BCE可以得出∠EAD=∠CBE,有BC=AC,由平角的定义可以得出∠BCD=60°,就有∠ACB=∠BCD,可以得出△BCN≌△ACM,就可以得出CM=CN,从而得到△CMN为等边三角形,就有∠CMN=60°,得出∠CMN=∠ACB,就得出MN∥AE.
(3)由△CMN为等边三角形,就有MN=CN,由条件可以得出CN∥AB,设CE=x,就可以用相似三角形的性质把CN用含x的函数式表示出来,从而求出其C点的位置进和最大值.
(2)由△ACD≌△BCE可以得出∠EAD=∠CBE,有BC=AC,由平角的定义可以得出∠BCD=60°,就有∠ACB=∠BCD,可以得出△BCN≌△ACM,就可以得出CM=CN,从而得到△CMN为等边三角形,就有∠CMN=60°,得出∠CMN=∠ACB,就得出MN∥AE.
(3)由△CMN为等边三角形,就有MN=CN,由条件可以得出CN∥AB,设CE=x,就可以用相似三角形的性质把CN用含x的函数式表示出来,从而求出其C点的位置进和最大值.
解答:解:∵△ABC和△CDE为等边三角形,
∴BC=AC,DC=EC,∠ACB=∠DCE=60°.
∴,∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中
∵
,
∴△ACD≌△BCE,
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠EAD=∠CBE.
∵∠ACB+∠BCD+∠DCE=180°,且∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACB=∠BCD.
在△BCN和△ACM中
∵
.
∴△BCN≌△ACM,
∴CM=CN,且∠BCD=60°,
∴△CMN是等边三角形.
∴∠CMN=60°,
∴∠CMN=∠ACB,
∴MN∥AE.
(3)∵△CMN是等边三角形,
∴CN=MN.
∵,∠ACB=∠DCE=60°,
∴CD∥AB,
∴△CEN∽△AEB,
∴
=
.
设CE为x,则有AC=AB=8-x.
∴
=
,
∴NC=x-
x2.
∴NC=-
(x-4)2+2,
∴当x=4时,NC有最大值是2.
即点C在AE的中点时,线段MN最大,最大值是2.
∴BC=AC,DC=EC,∠ACB=∠DCE=60°.
∴,∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE.
在△ACD和△BCE中
∵
|
∴△ACD≌△BCE,
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠EAD=∠CBE.
∵∠ACB+∠BCD+∠DCE=180°,且∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACB=∠BCD.
在△BCN和△ACM中
∵
|
∴△BCN≌△ACM,
∴CM=CN,且∠BCD=60°,
∴△CMN是等边三角形.
∴∠CMN=60°,
∴∠CMN=∠ACB,
∴MN∥AE.
(3)∵△CMN是等边三角形,
∴CN=MN.
∵,∠ACB=∠DCE=60°,
∴CD∥AB,
∴△CEN∽△AEB,
∴
| CN |
| AB |
| CE |
| AE |
设CE为x,则有AC=AB=8-x.
∴
| CN |
| 8-x |
| x |
| 8 |
∴NC=x-
| 1 |
| 8 |
∴NC=-
| 1 |
| 8 |
∴当x=4时,NC有最大值是2.
即点C在AE的中点时,线段MN最大,最大值是2.
点评:本题考查了平行线分线段成比例的运用,全等三角形的判定与性质,等边三角形的性质,以及二次函数的最值的运用.在解答的过程中书写全等三角形时对应顶点的字母要写在对应的位置上,灵活运用顶点式求最值.

练习册系列答案
相关题目
 如图,已知点C为线段AE的中点,∠A=∠E,∠ACB=∠ECD.
如图,已知点C为线段AE的中点,∠A=∠E,∠ACB=∠ECD.
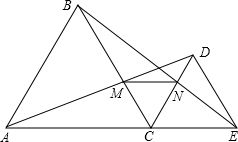 如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.
如图,已知点C为线段AE上一点,AE=8cm,△ABC和△CDE为AE同侧的两个等边三角形,连接BE交CD于N,连接AD交BC于M,连接MN.