题目内容
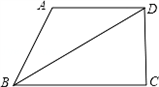
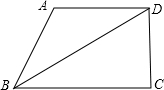 如图所示,已知BD平分∠ABC,∠C=62°,∠ABD=30°,∠ADC=118°,求∠A的度数.
如图所示,已知BD平分∠ABC,∠C=62°,∠ABD=30°,∠ADC=118°,求∠A的度数.分析:根据平行线的判定定理(同旁内角互补,两直线平行)推知AD∥BC,然后利用角平分线的性质、平行线的性质以及三角形内角和是180°即可求得∠A的度数.
解答:解:∵∠C=62°,∠ADC=118°,
∴∠C+∠ADC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠ADB=∠BDC(两直线平行,内错角相等);
又∵BD平分∠ABC,∠ABD=30°,
∴∠ABD=∠DBC=∠ADB=30°,
∴∠A=180°-∠ABD-∠ADB=120°(三角形内角和定理),
即∠A=120°.
∴∠C+∠ADC=180°,
∴AD∥BC(同旁内角互补,两直线平行),
∴∠ADB=∠BDC(两直线平行,内错角相等);
又∵BD平分∠ABC,∠ABD=30°,
∴∠ABD=∠DBC=∠ADB=30°,
∴∠A=180°-∠ABD-∠ADB=120°(三角形内角和定理),
即∠A=120°.
点评:本题考查了平行线的判定与性质.解答该题时,需要找出隐含在题干中的已知条件△ABD的内角和是180°.

练习册系列答案
相关题目


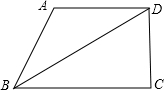 如图所示,已知BD平分∠ABC,∠C=62°,∠ABD=30°,∠ADC=118°,求∠A的度数.
如图所示,已知BD平分∠ABC,∠C=62°,∠ABD=30°,∠ADC=118°,求∠A的度数.