题目内容
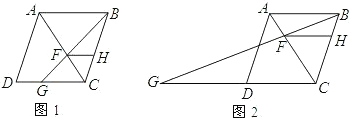
如图①,已知四边形ABCD是正方形,点E是AB的中点,点F在边CB的延长线上,且BE=BF,连接EF.
(1)若取AE的中点P,求证:BP=
CF;
(2)在图①中,若将△BEF绕点B顺时针方向旋转α(0<α<360°),如图②,是否存在某位置,使得AE∥BF?若存在,求出所有可能的旋转角α的大小;若不存在,请说明理由.

(1)若取AE的中点P,求证:BP=
| 1 | 2 |
(2)在图①中,若将△BEF绕点B顺时针方向旋转α(0<α<360°),如图②,是否存在某位置,使得AE∥BF?若存在,求出所有可能的旋转角α的大小;若不存在,请说明理由.

分析:(1)设正方形的边长为4a,则BE=AE=2a,由BE=BF得到BF=2a,所以CF=6a,由点P为AE的中点得EP=a,则BP=3a,由此得到BP=
CF;
(2)由(1)得到BE=BF=
AB,∠EBF=90°,当AE∥BF时,则∠AEB=∠EBF=90°,所以∠BAE=30°,则∠ABE=60°,即α=60°,易得α=300°时,AE∥BF.
| 1 |
| 2 |
(2)由(1)得到BE=BF=
| 1 |
| 2 |
解答:(1)证明:设正方形的边长为4a,
∵点E是AB的中点,
∴BE=AE=2a,
∵BE=BF,
∴BF=2a,
∴CF=4a+2a=6a,
∵点P为AE的中点,
∴EP=a,
∴BP=2a+a=3a,
∴BP=
CF;
(2)存在.
∵AE∥BF,
而BE=BF=
AB,∠EBF=90°,
∴∠AEB=∠EBF=90°,
∴∠BAE=30°,
∴∠ABE=60°,即α=60°,
当△BEF绕点B逆时针方向旋转60°时,AE∥BF,此时α=300°,
∴旋转角α为60°或300°.
∵点E是AB的中点,
∴BE=AE=2a,
∵BE=BF,
∴BF=2a,
∴CF=4a+2a=6a,
∵点P为AE的中点,
∴EP=a,
∴BP=2a+a=3a,
∴BP=
| 1 |
| 2 |
(2)存在.
∵AE∥BF,
而BE=BF=
| 1 |
| 2 |
∴∠AEB=∠EBF=90°,
∴∠BAE=30°,
∴∠ABE=60°,即α=60°,
当△BEF绕点B逆时针方向旋转60°时,AE∥BF,此时α=300°,
∴旋转角α为60°或300°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目