��Ŀ����
����Ŀ������֪������������ȵ������ν������������Σ����Ƶģ����Ƕ��壺������һ��Ա���ȵ��ı��ν����ȶԱ��ı��Σ�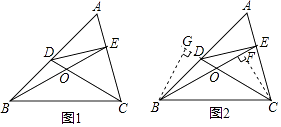
��1����д��һ����ѧ�����ı������ǵȶԱ��ı��ε�ͼ�ε����ƣ�
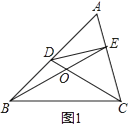
��2����ͼ1���ڡ�ABC�У���D��E�ֱ���AB��AC�ϣ���CD��BE�ཻ�ڵ�O������A=60�㣬��DCB=��EBC= ![]() ��A������д�����A��ȵĽǣ�
��A������д�����A��ȵĽǣ�
��3��������֤ͼ�е��ı���BCED�ǵȶԱ��ı��Σ�
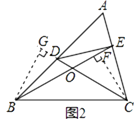
����ʾ����ͼ2����֤��BGO�ա�CFO��֤��BGD�ա�CFE���ɵõ�����BD=CE������֤����
���ڡ�ABC�У������A�Dz�����60�����ǣ�D��E�ֱ���AB��AC�ϣ���CD��BE�ཻ�ڵ�O����DCB=��EBC= ![]() ��A��̽������������������ͼ�����Ƿ���ڵȶԱ��ı��Σ���֤����Ľ��ۣ�
��A��̽������������������ͼ�����Ƿ���ڵȶԱ��ı��Σ���֤����Ľ��ۣ�
���𰸡�
��1���⣺ƽ���ı��εȣ�ֻҪ�Ա���ȼ��ɣ�
��2���⣺�ߡ�A=60�㣬��DCB=��EBC= ![]() ��A��
��A��
���OBC=��OCB=30�㣬
���BOD=��EOC=��OBC+��OCB=60�㣬
�����A��ȵĽ��ǡ�BOD����EOC
��3���⣺���ۣ��ı���BCED�ǵȶԱ��ı��Σ��������£�
��ͼ2�У���BG��CD��G��CF��BE��F��
�ߡ�DCB=��EBC= ![]() ��A��
��A��
��OB=OC��
�ڡ�BGO�͡�CFO�У�
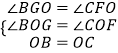 ��
��
���BGO�ա�CFO��
��BG=CF��
�ߡ�BOD=��A��
���A+��DOE=180�㣬��ADO+��AEO=180�㣬
�ߡ�AEO+��CEF=180�㣬��ADO=��BDG��
���BDG=��CEF���ߡ�BGD=��CFE��
���BGD�ա�CFE��
��BD=CE��
���BGD�ա�CFE��
��BD=CE��
���ı���BCED�ǵȶԱ��ı���
����������1�����ݵȶԱ��ı��εĶ�������жϼ��ɣ�
��2�����������ε���ǵ����ʣ������BOD���ɽ�����⣻
��3����֤��BGO�ա�CFO��֤��BGD�ա�CFE���ɵõ�����BD=CE.