题目内容
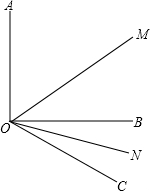 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.(2)若(1)中∠AOB=α°,其它条件不变,求∠MON的度数.
(3)若(1)中∠BOC=β°(β为锐角),其它条件都不变(∠AOB仍是90°),求∠MON的度数.
(4)从(1)(2)(3)的结果中能看出什么规律?
分析:(1)先计算出∠AOC=∠AOB+∠BOC=90°+30°=120°,再根据角平分线的定义得到∠COM=
∠AOC=
×120°=60°,∠CON=
∠BOC=
×30°=15°,然后利用
∠MON=∠COM-∠CON进行计算;
(2)先计算出∠AOC=∠AOB+∠BOC=a°+30°,再根据角平分线的定义得到∠COM=
∠AOC=
(a°+30°),∠CON=
∠BOC=
×30°=15°,然后利用
∠MON=∠COM-∠CON进行计算;
(3)先得到∠AOC=90°+β,再根据角平分线的定义得到∠COM=
∠AOC=
(90°+β),∠CON=
∠BOC=
β,然后利用
∠MON=∠COM-∠CON进行计算;
(4)利用前面计算的结论得到∠MON=
∠AOB.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠MON=∠COM-∠CON进行计算;
(2)先计算出∠AOC=∠AOB+∠BOC=a°+30°,再根据角平分线的定义得到∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠MON=∠COM-∠CON进行计算;
(3)先得到∠AOC=90°+β,再根据角平分线的定义得到∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠MON=∠COM-∠CON进行计算;
(4)利用前面计算的结论得到∠MON=
| 1 |
| 2 |
解答:解:(1)因为∠AOB=90°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
∠AOC=
×120°=60°,
∠CON=
∠BOC=
×30°=15°.
所以∠MON=∠COM-∠CON=60°-15°=45°;
(2)因为∠AOB=a°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=a°+30°.
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
∠AOC=
(a°+30°),
∠CON=
∠BOC=
×30°=15°.
所以∠MON=∠COM-∠CON=
(a°+30°)-15°=
a°.…(2分)
(3)因为∠AOB=90°,∠BOC=β,所以∠AOC=90°+β,
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
∠AOC=
(90°+β),∠CON=
∠BOC=
β.
所以∠MON=∠COM-∠CON=
(90°+β)-
β=45°.…..(2分)
(4)从(1)(2)(3)的结果中可以看出∠MON=
∠AOB,而与∠BOC的大小无关.
所以∠AOC=∠AOB+∠BOC=90°+30°=120°.
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠MON=∠COM-∠CON=60°-15°=45°;
(2)因为∠AOB=a°,∠BOC=30°,
所以∠AOC=∠AOB+∠BOC=a°+30°.
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠MON=∠COM-∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
(3)因为∠AOB=90°,∠BOC=β,所以∠AOC=90°+β,
又OM平分∠AOC,ON平分∠BOC,
所以∠COM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以∠MON=∠COM-∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
(4)从(1)(2)(3)的结果中可以看出∠MON=
| 1 |
| 2 |
点评:本题考查了角的计算:利用几何图形计算几个角的和或差.也考查了角平分线的定义.

练习册系列答案
相关题目
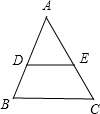 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
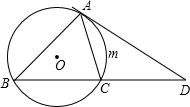 =2,∠ADC=30°
=2,∠ADC=30°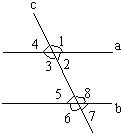 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
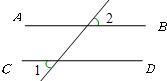 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=