题目内容
已知△ABC 是等边三角形.
(1 )将△ABC 绕点A 逆时针旋转角(0 °<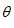 <180 °),得到△ADE ,BD 和EC 所在直线相交于点O.
<180 °),得到△ADE ,BD 和EC 所在直线相交于点O.
①如图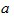 ,当
,当 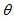 =20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度;
=20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度;
②当△AB C旋转到如图
C旋转到如图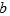 所在位置时,求∠BOE的度数;
所在位置时,求∠BOE的度数;
(2)如图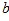 ,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<
,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<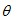 <180°),得到△ADE
<180°),得到△ADE
(3)BD和EC所在直线相交于点O,请利用图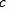 探索∠BOE的度数,直接写出结果,不必说明理由.
探索∠BOE的度数,直接写出结果,不必说明理由.
(1 )将△ABC 绕点A 逆时针旋转角(0 °<
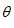 <180 °),得到△ADE ,BD 和EC 所在直线相交于点O.
<180 °),得到△ADE ,BD 和EC 所在直线相交于点O. ①如图
 ,当
,当 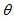 =20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度;
=20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度;②当△AB
 C旋转到如图
C旋转到如图 所在位置时,求∠BOE的度数;
所在位置时,求∠BOE的度数; (2)如图
 ,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<
,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<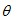 <180°),得到△ADE
<180°),得到△ADE (3)BD和EC所在直线相交于点O,请利用图
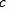 探索∠BOE的度数,直接写出结果,不必说明理由.
探索∠BOE的度数,直接写出结果,不必说明理由.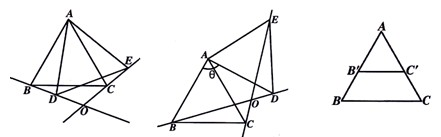
解:(1 )是
∠BOE=120°
(2)由已知得:△ABC和△ADE是全等的等边三角形
∴AB=AD=AC=AE
∵△ADE 是由△ABC 绕点A 旋转 得到的
得到的
∴∠BAD= ∠CAE=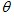
∴△BAD ≌△CAE
∴∠ADB= ∠AEC
∵∠ADB+ ∠ABD+ ∠BAD=180 °
∴∠AEC+ ∠ABO+∠BAD=180°
∵∠ABO+∠AEC+∠BAE+∠BOE=360°
∵∠BAE=∠BAD+∠DAE
∴∠DAE+∠BOE=180°
又∵∠DAE=60°
∴∠BOE=120°
(3 )当0 °<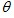 <30 °时,∠BOE=60 °
<30 °时,∠BOE=60 °
当30 °< <180 °时,∠BOE=120 °
<180 °时,∠BOE=120 °
∠BOE=120°
(2)由已知得:△ABC和△ADE是全等的等边三角形
∴AB=AD=AC=AE
∵△ADE 是由△ABC 绕点A 旋转
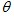 得到的
得到的 ∴∠BAD= ∠CAE=
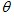
∴△BAD ≌△CAE
∴∠ADB= ∠AEC
∵∠ADB+ ∠ABD+ ∠BAD=180 °
∴∠AEC+ ∠ABO+∠BAD=180°
∵∠ABO+∠AEC+∠BAE+∠BOE=360°
∵∠BAE=∠BAD+∠DAE
∴∠DAE+∠BOE=180°
又∵∠DAE=60°
∴∠BOE=120°
(3 )当0 °<
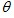 <30 °时,∠BOE=60 °
<30 °时,∠BOE=60 °当30 °<
 <180 °时,∠BOE=120 °
<180 °时,∠BOE=120 °
练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
 如图,已知△ABC是等边三角形,点D,B,C,E在同一直线上,
如图,已知△ABC是等边三角形,点D,B,C,E在同一直线上, 如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.
如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.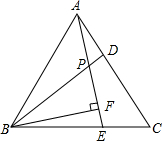 如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.若BP=6,求PF的长.
如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.若BP=6,求PF的长. 如图,已知△ABC是等边三角形,点O是BC上任意一点,OE,OF分别于两边垂直,等边三角形的高为2,则OE+OF的值为( )
如图,已知△ABC是等边三角形,点O是BC上任意一点,OE,OF分别于两边垂直,等边三角形的高为2,则OE+OF的值为( )