Question

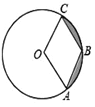
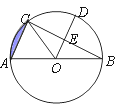
【题目】如图，在△ABC中，∠C=90°，AE平分∠BAC交BC于E，点O在AB上，以OA为半径的圆，交AB于D，交AC于C，且点E在⊙O上，连接DE，BF切⊙O于点F．

(1)求证：BE=BF；

(2)若⊙O的半径为R，AG=R+1，CE=R﹣1，求弦AG的长．

Answer 1

【答案】(1)证明见解析；(2)AG=6.

【解析】

（1）连接OE，证出OE⊥CD，再由切线长定理易得BE=BF；
（2）根据直径所对的圆周角得出∠AGD=90°，从而证得GD∥BC，进而证得OE⊥GD，根据垂径定理得出GH=DH，然后证得四边形GCEH是矩形，从而证得GD=2（R-1）=2R-2，最后根据勾股定理求得R，即可求得AG的长．

(1)连接DG、OE，交于点H．

∵AE平分∠BAC交BC于E，

∴∠CAE=∠DAE，

∵OA=OE，

∴∠OAE=∠OEA，

∴∠CAE=∠OEA，

∴AC∥OE，

∴∠OEB=∠C=90°，

∴OE⊥BC，

∴BC是圆的切线，

∴BE=BF；

(2)∵AB是直径，

∵∠AGD=90°，

∵∠C=90°，

∴GD∥BC，

∵OE⊥BC，

∴OE⊥GD，

∴GH=DH，

∵∠AGD=90°，∠C=90°，OE⊥BC，

∴四边形GCEH是矩形，

∴GH=CE=R﹣1，

∴GD=2（R﹣1）=2R﹣2，

在直角三角形AGD中，AG2+GD2=AD2 ，

即（R+1）2+（2R﹣2）2=（2R）2

解得R1=5，R2=1（舍去），

∴AG=R+1=5+1=6；