题目内容
【题目】已知:如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接CD,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
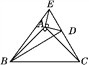
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】如图:
①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE.
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴①正确;
②∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ABD+∠DBC=45°.
∴∠ACE+∠DBC=45°,
∴②正确;
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵∠CAB=90°,
∴∠ABD+∠AFB=90°,
∴∠ACE+∠AFB=90°.
∵∠DFC=∠AFB,
∴∠ACE+∠DFC=90°,
∴∠FDC=90°.
∴BD⊥CE,
∴③正确;
④∵∠BAC=∠DAE=90°,∠BAC+∠DAE+∠BAE+∠DAC=360°,
∴∠BAE+∠DAC=180°,故④正确.
所以①②③④都正确,共计4个.
故选D.

练习册系列答案
相关题目
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③ B.②③④ C.②③ D.①④