Question

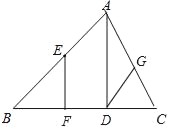
【题目】已知：如图，在△ABC中，过点A作AD⊥BC，垂足为D，E为AB上一点，过点E作EF⊥BC，垂足为F，过点D作DG∥AB交AC于点G．

（1）依题意补全图形；

（2）请你判断∠BEF与∠ADG的数量关系，并加以证明．

Answer 1

【答案】（1）见解析（2）∠BEF＝∠ADG

【解析】

（1）根据题意画出图形即可；

（2）证出AD∥EF，得出∠BEF＝∠BAD，再由平行线的性质得出∠BAD＝∠ADG，即可得出结论．

解：（1）如图所示：

（2）∠BEF＝∠ADG．理由如下：

∵AD⊥BC，EF⊥BC，

∴∠ADF＝∠EFB＝90°．

∴AD∥EF（同位角相等，两直线平行）．

∴∠BEF＝∠BAD（两直线平行，同位角相等）．

∵DG∥AB，

∴∠BAD＝∠ADG（两直线平行，内错角相等）．

∴∠BEF＝∠ADG．