题目内容
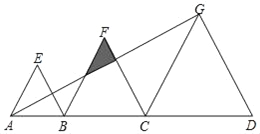
【题目】如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
①CD=____;
②图中阴影部分面积为_____.
【答案】10 ![]()
![]()
【解析】
①利用相似三角形对应边成比例列式计算即可得解;
②设AG与CF、BF分别相交于点M、N,根据等边对等角求出∠CAG=∠CGA,再利用三角形的一个外角等于与它不相邻的两个内角的和求出∠CGA=30°,然后求出AG⊥GD,再根据相似三角形对应边成比例求出CM,从而得到MF,然后求出MN,再利用三角形的面积公式列式计算即可得解.
①解:∵△ABE、△CDG都是等边三角形,
∴△ABE∽△CDG,
∴![]()
即![]() ,
,
解得CD=10;
②解:如图,设AG与CF、BF分别相交于点M、N,

∵AC=AB+BC=4+6=10,
∴AC=CG,
∴∠CAG=∠CGA,
又∵∠CAG+∠CGA=∠DCG=60°,
∴∠CGA=30°,
∴∠AGD=∠CGA+∠CGD=30°+60°=90°,
∴AG⊥GD,
∵∠BCF=∠D=60°,
∴CF∥DG,
∴△ACM∽△ADG,
∴MN⊥CF,
![]() ,
,
即![]() ,
,
解得CM=5,
所以,MF=CFCM=65=1,
∵∠F=60°,
∴MN=![]() MF=
MF=![]() ,
,
∴S△MNF=![]() MFMN=
MFMN=![]() ×1×
×1×![]() =
=![]() ,
,
即阴影部分面积为![]() .
.
故答案为:10;![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目