题目内容
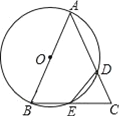
【题目】如图,AB是⊙O的直径,C是![]() 的中点,CE⊥AB于点E,BD交CE于点F.
的中点,CE⊥AB于点E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=5,AC=12,求⊙O的半径和CE的长.

【答案】(1)证明见解析;(2)CE=![]() .
.
【解析】
(1)由AB是⊙O的直径,根据直径所对的圆周角是直角即可得∠ACB=90°,又由CE⊥AB,根据同角的余角相等可证得∠BCE =∠A,又由C是![]() 的中点,证得∠DBC =∠A,继而可证得CF﹦BF;(2)由C是
的中点,证得∠DBC =∠A,继而可证得CF﹦BF;(2)由C是![]() 的中点和CD=5可求得BC=5,利用勾股定理求得AB=13,即可求得⊙O的半径为6.5;在Rt△ACB中,利用三角形面积的两种表示方法即可求得EC的长.
的中点和CD=5可求得BC=5,利用勾股定理求得AB=13,即可求得⊙O的半径为6.5;在Rt△ACB中,利用三角形面积的两种表示方法即可求得EC的长.
(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∴∠A+∠ABC=90°.
又∵CE⊥AB,
∴∠CEB=90°.
∴∠BCE+∠ABC=90°.
∴∠BCE=∠A,
∵C是![]() 的中点,
的中点,
∴![]() =
=![]() .
.
∴∠DBC=∠A,
∴∠DBC=∠BCE.
∴CF=BF;
(2)∵![]() =
=![]() ,CD=5,
,CD=5,
∴BC=CD=5,
∴AB=![]() =13,
=13,
∴⊙O的半径为6.5,
∵![]() CEAB=
CEAB=![]() ACBC,
ACBC,
∴CE=![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】下表是二次函数![]() 的部分
的部分![]() 的对应值:
的对应值:
x | … | -1 |
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … | m |
| -1 |
| -2 |
| -1 |
| 2 | … |
(1)求函数解析式;
(2)当![]() 时,y的取值范围是___________;
时,y的取值范围是___________;
(3)当抛物线![]() 的顶点在直线
的顶点在直线![]() 的下方时,n的取值范围是__________.
的下方时,n的取值范围是__________.