题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB. 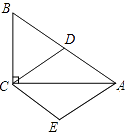
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
【答案】
(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD= ![]() AB=BD=AD,
AB=BD=AD,
∴平行四边形ADCE是菱形
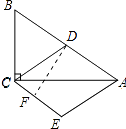
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CDsin60°=6× ![]() =3
=3 ![]() .
.
【解析】(1)先证明四边形ADCE是平行四边形,再证出一组邻边相等,即可得出结论;(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.

【题目】请你用学习“一次函数”时积累的经验和方法解决下列问题:
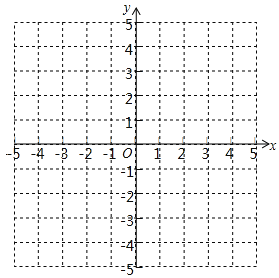
(1)在平面直角坐标系中,画出函数y=|x|的图象;
①列表填空:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | … |
②描点、连线,在图所示的平面直角坐标系中画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|的两条不同类型的性质.
【题目】2022年将在北京﹣﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1 | 队员2 | 队员3 | 队员4 | 队员5 | 队员6 | |
甲组 | 176 | 177 | 175 | 176 | 177 | 175 |
乙组 | 178 | 175 | 170 | 174 | 183 | 176 |
设两队队员身高的平均数依次为 ![]() 甲 ,
甲 , ![]() 乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
A.![]() 甲=
甲= ![]() 乙 , S甲2<S乙2
乙 , S甲2<S乙2
B.![]() 甲=
甲= ![]() 乙,S甲2>S乙2
乙,S甲2>S乙2
C.![]() 甲<
甲< ![]() 乙 , S甲2<S乙2
乙 , S甲2<S乙2
D.![]() 甲>
甲> ![]() 乙 , S甲2>S乙2
乙 , S甲2>S乙2