Question

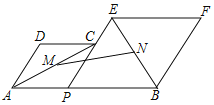
【题目】如图，已知AB=12，P为线段AB上的一个动点，分别以AP、PB为边在AB的同侧作菱形APCD和菱形PBFE，点P、C、E在一条直线上，∠DAP=60°．M、N分别是对角线AC、BE的中点．当点P在线段AB上移动时，点M、N之间的距离最短为______．（结果留根号）

Answer 1

【答案】

【解析】

连接MP，NP，证明MP⊥NP，将M、N的距离转化为直角三角形的斜边最短，利用勾股定理结合二次函数即可求解；

解：连接MP，NP，

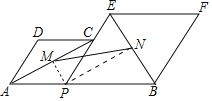
∵菱形APCD和菱形PBFE，∠DAP=60°，

∴MP=AP，NP=BP，

∵M、N分别是对角线AC、BE的中点，

∴∠MPC=60°，∠EPN=30°，

∴MP⊥NP，

∴MN2=MP2+NP2，

即MN2=（AP）2+（BP）2=[AP2+（12-AP）2]= （AP2-12AP+72）=（AP-6）2+18，

当AP=6时，MN有最小值3，

∴点M、N之间的距离最短为3；

故答案为3；