题目内容
【题目】如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y(其中x>y)表示小矩形的长与宽,请观察图案,指出以下关系式中不正确的是( )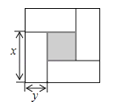
A.x+y=7
B.x﹣y=2
C.x2﹣y2=4
D.4xy+4=49
【答案】C
【解析】解:A、因为正方形图案的边长7,同时还可用(x+y)来表示,故此选项正确;
B、中间小正方形的边长为2,同时根据长方形长宽也可表示为x﹣y,故此选项正确;
C、根据A、B可知x+y=7,x﹣y=2,则x2﹣y2=(x+y)(x﹣y)=14,故此选项错误;
D、因为正方形图案面积从整体看是49,从组合来看,可以是(x+y)2 , 还可以是(4xy+4),即4xy+4=49,故此选项正确;
故选:C.
分别根据大正方形边长、小正方形边长的不同表示可判断A、B,由A、B结论利用平方差公式可判断C,根据大正方形面积的整体与组合的不同表示可判断D.

练习册系列答案
相关题目