题目内容
【题目】在平面直角坐标系xOy中，点P的坐标为（a，b），点P的“关联点”P’的坐标定义如下：当
时，P’点坐标为（b，a）；当
时，P’点坐标为（－a，－b）．
（1）写出A（5，3）的变换点坐标_____，B（1，6）的变换点坐标______，C（－2，4）的变换点坐标_____；
（2）如果直线l：
上所有点的关联点组成一个新的图形，记作图形W，请画出图形W；
（3）在（2）的条件下，若直线y=kx－1（k≠0）与图形W有两个交点，请直接写出k的取值范围．
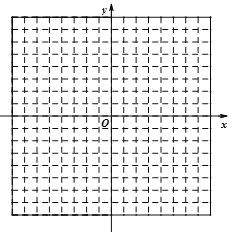
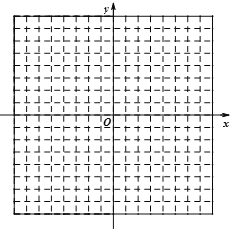
【答案】（1）A(3,5)，B(-1,-6)，C(2,-4)；（2）见详解；（3）
或
【解析】
（1）根据A、B、C三点的横、纵坐标间的关系即可找出与之对应的变换点坐标；
（2）根据直线DE的解析式，找出横纵坐标相等的点的坐标，根据变换点的定义，将直线DE上的点（2，2）左侧（不包括该点）的射线作关于原点对称的射线，再将直线DE的点（2，2）右侧（包括该点）作关于x=y对称的射线，由此即可得出图形W；
（3）根据W的做法找出图形W中两段射线的解析式，分别令y＝kx1（k≠0）与这两段射线的交点的横坐标满足射线中x的取值范围，综合在一起即可得出结论．
解：（1）∵5＞3，1＜6，-2＜4，
∴A(3,5)，B(-1,-6)，C(2,-4)；
（2）当x=y时，则有
，解得x=y=2，∴将直线DE上的点(2,2)右侧(包括该点)的射线作关于x=y对称的射线；再将直线DE上的点(2,2)左侧(不包括该点)作关于原点对称的射线，由此即可得出图形W;
（3）经过变换得到的两条射线方程为：
y=-2x+6 (x≤2)
(x＞-2)
令-2x+6=kx-1(k≠0)，则有
且k≠0，k≠-2
解得：或k<-2
令
(k≠0)，则有
且k≠0，2k+1≠0
解得：
或
综上可知: 若直线y=kx－1（k≠0）与图形W有两个交点，k的取值范围为：或k<-2
