Question

阅读下面材料：
小明遇到这样一个问题：如图1，△ABO和△CDO均为等腰直角三角形，∠AOB=∠COD=90°．若△BOC的面积为1，试求以AD、BC、OC+OD的长度为三边长的三角形的面积．

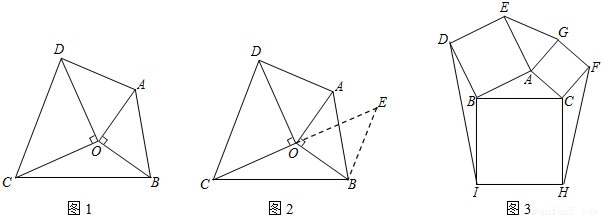
小明是这样思考的：要解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可．他利用图形变换解决了这个问题，其解题思路是延长CO到E，使得OE=CO，连接BE，可证△OBE≌△OAD，从而得到的△BCE即是以AD、BC、OC+OD的长度为三边长的三角形（如图2）．
请你回答：图2中△BCE的面积等于______．
请你尝试用平移、旋转、翻折的方法，解决下列问题：
如图3，已知△ABC，分别以AB、AC、BC为边向外作正方形ABDE、AGFC、BCHI，连接EG、FH、ID．
（1）在图3中利用图形变换画出并指明以EG、FH、ID的长度为三边长的一个三角形（保留画图痕迹）；
（2）若△ABC的面积为1，则以EG、FH、ID的长度为三边长的三角形的面积等于______．

Answer 1

【答案】分析：由等腰直角三角形的性质、旋转的性质知，△OEB与△BOC是等底同高的两个三角形；
①将△DBI和△FCH平移即可得到如图所示的△EGM．
②如图2，根据正方形的性质推知△ABE和△ACG都是等腰直角三角形，则根据旋转的性质推知S_△AEG=S_△AEM=S_△AMG=S_△ABC=1，所以易求△EGM的面积．
解答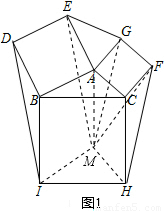：解：∵△ABO和△CDO均为等腰直角三角形，∠AOB=∠COD=90°，
∴OD=OC，OA=OB．
又∵将△AOD绕点O顺时针旋转90°得△OBE，
∴∠DOE=90°，OD=OE，
∴点C、O、E三点共线，
∵OC=OE，
∴△OEB与△BOC是等底同高的两个三角形，
∴S_△OEB=S_△BOC=1，
∴S_△BCE=S_△OEB+S_△BOC=2．

①（答案不唯一）：如图1，
以EG、FH、ID的长度为三边长的一个三角形是△EGM．

②如图2，∵四边形AEDB和四边形ACFG都是正方形，
∴△ABE和△ACG都是等腰直角三角形，
∴S_△AEG=S_△AEM=S_△AMG=S_△ABC=1，
∴S△EGM=S_△AEG+S_△AEM+S_△AMG=3，即以EG、FH、ID的长度为三边长的三角形的面积等于3．
故答案是：2，3．
点评：本题考查了全等三角形的判定与性质、三角形的面积、等腰三角形的性质以及正方形的性质．注意平移、旋转的性质的应用．