��Ŀ����
�ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ�٢ڢ��е�һ�֣�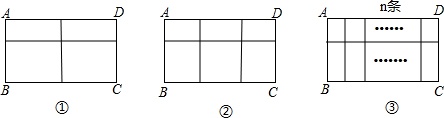
������AB=x�ף����������ͼ���ش��������⣺�����еIJ���ֲ����ܳ��Ⱦ�ָ��ͼ�����к��ߵij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�
��1����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2����ͼ���У�������ոֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����μ�ABCD�����S����������Ƕ��٣�
��3����ͼ���У��������ֲ����ܳ���Ϊa�ף�����n����������ô��xΪ����ʱ�����ο��ABCD�����S����������Ƕ��٣�
��������1�����ú�x�Ĵ���ʽ��12-3x����3=4-x��ʾ�ᵵAD�ij���Ȼ����ݾ��ε������ʽ�з��̣����x��ֵ��
��2���ú�x�Ĵ���ʽ��12-4x����3=4-
x��ʾ�ᵵAD�ij���Ȼ����ݾ��������ʽ�õ����κ��������ö��κ��������ʣ�������ε��������Լ���Ӧ��x��ֵ��
��3���ú�x�Ĵ���ʽ��a-nx����3=
-
x��ʾ�ᵵAD�ij���Ȼ����ݾ��ε������ʽ�õ����κ��������ö��κ��������ʣ�������ε��������Լ���Ӧ��x��ֵ��
��2���ú�x�Ĵ���ʽ��12-4x����3=4-
| 4 |
| 3 |
��3���ú�x�Ĵ���ʽ��a-nx����3=
| a |
| 3 |
| n |
| 3 |
����⣺��1��AD=��12-3x����3=4-x��
�з��̣�x��4-x��=3��
x2-4x+3=0��
��x1=1��x2=3��
�𣺵�x=1��3��ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2��AD=��12-4x����3=4-
x��
S=x��4-
x����
=-
x2+4x��
��x=-
=
ʱ��
S���=
=3��
�𣺵�x=
ʱ�����μ�ABCD�����S�����������3ƽ���ף�
��3��AD=��a-nx����3=
-
x��
S=x��
-
x����
=-
x2+
x��
��x=-
=
ʱ
S���=
=
��
�𣺵�x=
ʱ������ABCD�����S�����������
ƽ���ף�
�з��̣�x��4-x��=3��
x2-4x+3=0��
��x1=1��x2=3��
�𣺵�x=1��3��ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2��AD=��12-4x����3=4-
| 4 |
| 3 |
S=x��4-
| 4 |
| 3 |
=-
| 4 |
| 3 |
��x=-
| 4 | ||
2��(-
|
| 3 |
| 2 |
S���=
| 0-16 | ||
4��(-
|
�𣺵�x=
| 3 |
| 2 |
��3��AD=��a-nx����3=
| a |
| 3 |
| n |
| 3 |
S=x��
| a |
| 3 |
| n |
| 3 |
=-
| n |
| 3 |
| a |
| 3 |
��x=-
| ||
2��(-
|
| a |
| 2n |
S���=
-
| ||
4��(-
|
| a2 |
| 12n |
�𣺵�x=
| a |
| 2n |
| a2 |
| 12n |
���������⿼����Ƕ��κ�����Ӧ�ã���1�����������ʽ�з��̣����x��ֵ����2�����������ʽ�ö��κ��������ö��κ�������������ֵ����3�����������ʽ�õ���ĸϵ���Ķ��κ�����Ȼ��������������ֵ��

��ϰ��ϵ�д�
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
�����Ŀ

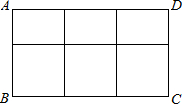 ��2012•�Ӷ���һģ���ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ������֪����ֲ����ܳ���Ϊ12�ף��������������������Ϊ������ʱ�����ο�ܵ��������������Ƕ���ƽ���ף������еIJ���ֲ����ܳ���ָͼ�������߶εij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�
��2012•�Ӷ���һģ���ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ������֪����ֲ����ܳ���Ϊ12�ף��������������������Ϊ������ʱ�����ο�ܵ��������������Ƕ���ƽ���ף������еIJ���ֲ����ܳ���ָͼ�������߶εij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�