题目内容
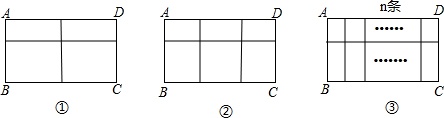
用长度一定的不锈钢材料设计成外观为矩形的框架(如图①②③中的一种)(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行,材料本身面积忽略不计),设竖档AB=x米,请根据以上图案回答下列问题:
(Ⅰ)在图①中,不锈钢材料总长度为12米,则AD表达式为______,若矩形框架ABCD的面积为3平方米,则可列方程为______.
(Ⅱ)在图②中,不锈钢材料总长度为12米,则AD表达式为______,若矩形框架ABCD的面积为S,请写出S与x的函数关系式______.
(Ⅲ)在图③中,如果不锈钢材料总长度为a米,共有n条竖档,写出矩形框架ABCD的面积S与x的函数关系式______;当x为______时,S有最大面积等于______.
【答案】分析:(I)由题意可得3AD+3AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出方程;
(II)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;
(III)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
解答:解:(I)AD=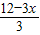 =4-x,则若矩形框架ABCD的面积为3平方米,则可列方程为:x(4-x)=3;
=4-x,则若矩形框架ABCD的面积为3平方米,则可列方程为:x(4-x)=3;
(II)AD=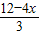 =4-
=4- x,
x,
S=x×(4- x)=4x-
x)=4x- x2;
x2;
(III)AD=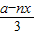 ,
,
S=AD×AB=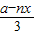 x=-
x=- x2+
x2+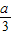 x=-
x=-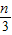 (x-
(x-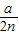 )2+
)2+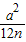 ,
,
当x=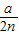 时,S有最大值,最大面积为
时,S有最大值,最大面积为 .
.
故答案为:4-x、x(4-x)=3;4- x、S=4x-
x、S=4x- x2;
x2;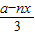 x、
x、 、
、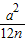 .
.
点评:本题考查了二次函数的应用,解答本题的关键是得出AD的表达式,根据矩形的面记公式得出函数解析式,注意掌握配方法求最值得应用.
(II)由题意可得3AD+4AB=12,从而可得出AD的表达式;根据矩形的面积=长×宽,可得出S与x的函数关系式;
(III)由题意可得3AD+nAB=a,从而可得出AD的表达式,根据矩形的面积=长×宽,可得出S与x的函数关系式,利用配方法可求出S的最大值.
解答:解:(I)AD=
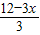 =4-x,则若矩形框架ABCD的面积为3平方米,则可列方程为:x(4-x)=3;
=4-x,则若矩形框架ABCD的面积为3平方米,则可列方程为:x(4-x)=3;(II)AD=
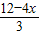 =4-
=4- x,
x,S=x×(4-
 x)=4x-
x)=4x- x2;
x2;(III)AD=
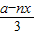 ,
,S=AD×AB=
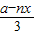 x=-
x=- x2+
x2+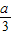 x=-
x=-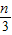 (x-
(x-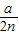 )2+
)2+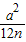 ,
,当x=
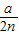 时,S有最大值,最大面积为
时,S有最大值,最大面积为 .
.故答案为:4-x、x(4-x)=3;4-
 x、S=4x-
x、S=4x- x2;
x2;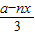 x、
x、 、
、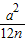 .
.点评:本题考查了二次函数的应用,解答本题的关键是得出AD的表达式,根据矩形的面记公式得出函数解析式,注意掌握配方法求最值得应用.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目

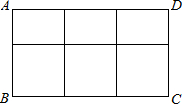 (2012•河东区一模)用长度一定的不锈钢材料设计成外观为矩形的框架(如图)现已知不锈钢材料总长度为12米,请你帮助分析,当竖档为多少米时,矩形框架的面积最大?最大面积是多少平方米?(题中的不锈钢材料总长度指图中所有线段的长度和,所有横档和竖档分别与AD、AB平行)
(2012•河东区一模)用长度一定的不锈钢材料设计成外观为矩形的框架(如图)现已知不锈钢材料总长度为12米,请你帮助分析,当竖档为多少米时,矩形框架的面积最大?最大面积是多少平方米?(题中的不锈钢材料总长度指图中所有线段的长度和,所有横档和竖档分别与AD、AB平行)