题目内容
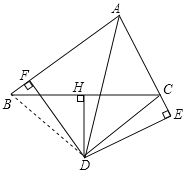
【题目】如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.

(1)求证:AD平分∠BAC;
(2)若∠BAC=80°,求∠DCB的度数.
【答案】(1)证明见试题解析;(2)40°.
【解析】
试题(1)连接BD,根据线段垂直平分线的性质可得BD=CD,再利用“HL”证明Rt△BDF和Rt△CDE全等,可得DE=DF,然后根据到角的两边距离相等的点在角的平分线上即可得到结论;
(2)根据全等三角形对应角相等可得∠CDE=∠BDF,求出∠BDC=∠EDF,再根据四边形的内角和定理求出∠EDF,然后根据等腰三角形两底角相等列式计算即可得解.
试题解析:(1)如图,连接BD,∵DH垂直平分BC,∴BD=CD,在Rt△BDF和Rt△CDE中,∵BD=CD,BF=CE,∴Rt△BDF≌Rt△CDE(HL),∴DE=DF,∵DF⊥AB于F,DE⊥AC,∴AD平分∠BAC;
(2)∵Rt△BDF≌Rt△CDE,∴∠CDE=∠BDF,∴∠BDC=∠EDF,∵∠BAC=80°,∴∠EDF=360°﹣90°×2﹣80°=100°,∴∠BDC=100°,∵BD=CD,∴∠DCB=![]() (180°﹣100°)=40°.
(180°﹣100°)=40°.

练习册系列答案
相关题目
【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价/(元·箱 | 销售价/(元·箱 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?