ЬтФПФкШн
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНЉx2+![]() x+4ЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
x+4ЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
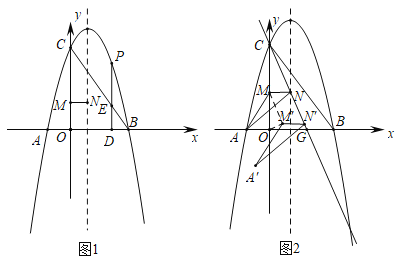
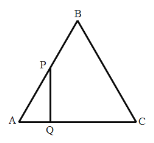
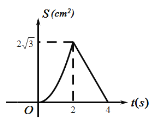
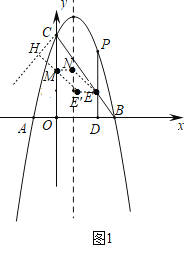
ЃЈ1ЃЉШчЭМ1ЃЌЕуPЪЧжБЯпBCЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїPDЁЭxжсНЛBCгкЕуEЃЌНЛxжсгкЕуDЃЎЕуMЮЊЯпЖЮOCЩЯвЛЖЏЕуЃЌЙ§ЕуMзїMNЁЮxжсНЛХзЮяЯпЕФЖдГЦжсгкЕуNЃЌЕБЫФБпаЮBOCPУцЛ§зюДѓЪБЃЌЧѓEN+MN+![]() CMЕФзюаЁжЕЃЎ
CMЕФзюаЁжЕЃЎ
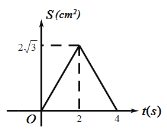
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌНЋЁїAMNдкжБЯпCNЩЯЦНвЦЃЌЕуMЕФЖдгІЕуЮЊЕуM'ЃЌЪЧЗёДцдкЕуM'ЪЙЕУЁїMOM'ГЩЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуM'ЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉEN+MN+![]() CMЕФзюаЁжЕЃН
CMЕФзюаЁжЕЃН![]() ЃЛЃЈ2ЃЉЕуMЁфЕФзјБъЮЊЃЈЉ
ЃЛЃЈ2ЃЉЕуMЁфЕФзјБъЮЊЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
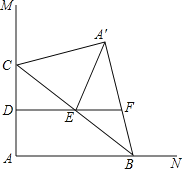
ЃЈ1ЃЉЕБЫФБпаЮBOCPУцЛ§зюДѓЪБЃЌжЛашвЊЁїBCPЕФУцЛ§SзюДѓЃЌДЫЪБЕуEЃЈ![]() ЃЌ2ЃЉЃЛЙ§ЕуEЁфзїEЁфHЁЭCHгкЕуHЃЌНЛyжсгкЕуMЃЌЙ§ЕуMзїMNЁЭХзЮяЯпЖдГЦжсНЛгкЕуNЃЌдђЕуMЁЂNЮЊЫљЧѓЃЌМДПЩЧѓНтЃЛ
ЃЌ2ЃЉЃЛЙ§ЕуEЁфзїEЁфHЁЭCHгкЕуHЃЌНЛyжсгкЕуMЃЌЙ§ЕуMзїMNЁЭХзЮяЯпЖдГЦжсНЛгкЕуNЃЌдђЕуMЁЂNЮЊЫљЧѓЃЌМДПЩЧѓНтЃЛ
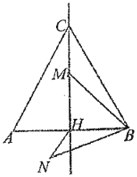
ЃЈ2ЃЉЗжMMЁфЃНOMЁЂMMЁфЃНOMЁфЁЂOMЁфЃНOMШ§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
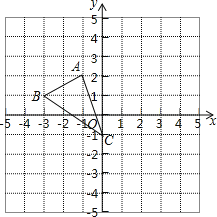
ЃЈ1ЃЉЖўДЮКЏЪ§yЃНЉx2+![]() x+4ЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌ
x+4ЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЌ
дђЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃКЃЈЉ![]() ЃЌ0ЃЉЁЂЃЈ3ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЛ
ЃЌ0ЃЉЁЂЃЈ3ЃЌ0ЃЉЁЂЃЈ0ЃЌ4ЃЉЃЛ
ЃЈ1ЃЉЕБЫФБпаЮBOCPУцЛ§зюДѓЪБЃЌжЛашвЊЁїBCPЕФУцЛ§SзюДѓЃЌ
гЩЕуBЁЂCЕФзјБъЕУжБЯпBCЕФБэДяЪНЮЊЃКyЃНЉ![]() x+4ЃЌ
x+4ЃЌ
ЩшЕуPЃЈxЃЌЉx2+![]() x+4ЃЉЃЌдђЕуEЃЈxЃЌЉ
x+4ЃЉЃЌдђЕуEЃЈxЃЌЉ![]() x+4ЃЉЃЌ
x+4ЃЉЃЌ
SЃН![]() ЁСPEЁСOBЃН
ЁСPEЁСOBЃН![]() ЃЈЉx2+
ЃЈЉx2+![]() x+4+
x+4+![]() xЉ4ЃЉЃН
xЉ4ЃЉЃН![]() ЃЈЉx2+3xЃЉЃЌ
ЃЈЉx2+3xЃЉЃЌ
ЕБxЃН![]() ЪБЃЌSзюДѓЃЌДЫЪБЕуEЃЈ
ЪБЃЌSзюДѓЃЌДЫЪБЕуEЃЈ![]() ЃЌ2ЃЉЃЛ
ЃЌ2ЃЉЃЛ
Й§ЕуCзїЁЯCMHЃНІСЃЌЪЙsinІСЃН![]() ЃЌ
ЃЌ
ХзЮяЯпЕФЖдГЦжсЮЊЃКxЃН![]() ЃЌдђMNЃН
ЃЌдђMNЃН![]() ЃЌ
ЃЌ
НЋЕуEЯђзѓЦНвЦMNЕФГЄЖШ![]() ИіЕЅЮЛЃЌЕУЕНЕуEЁфЃЈ
ИіЕЅЮЛЃЌЕУЕНЕуEЁфЃЈ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
Й§ЕуEЁфзїEЁфHЁЭCHгкЕуHЃЌНЛyжсгкЕуMЃЌЙ§ЕуMзїMNЁЭХзЮяЯпЖдГЦжсНЛгкЕуNЃЌдђЕуMЁЂNЮЊЫљЧѓЃЌ
СЌНгENЃЌЁпEEЁфЃНMNЃЌEEЁфЁЮMNЃЌ
ЁрEEЁфMNЮЊЦНааЫФБпаЮЃЌдђENЃНEЁфMЃЌ
EN+MN+![]() CMЕФзюаЁжЕЃНEЁфM+HM+MNЃНEЁфM+HM+
CMЕФзюаЁжЕЃНEЁфM+HM+MNЃНEЁфM+HM+![]() ЃЌ
ЃЌ
жБЯпHEЁфБэДяЪНжаЕФkЮЊЉ![]() ЃЌЕуEЁфЃЈ
ЃЌЕуEЁфЃЈ![]() ЃЌ2ЃЉЃЌ
ЃЌ2ЃЉЃЌ
дђжБЯпHEЁфЕФБэДяЪНЮЊЃКyЃНЉ![]() x+
x+![]() ЃЌ
ЃЌ
ЙЪЕуMЃЈ0ЃЌ![]() ЃЉЃЌЕуNЃЈ
ЃЉЃЌЕуNЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
EN+MN+![]() CMЕФзюаЁжЕЃНEЁфM+HM+
CMЕФзюаЁжЕЃНEЁфM+HM+![]() ЃН
ЃН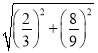 +
+![]() ЁСЃЈ4Љ
ЁСЃЈ4Љ![]() ЃЉ+
ЃЉ+![]() ЃН
ЃН![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕуMЃЈ0ЃЌ![]() ЃЉЃЌЕуNЃЈ
ЃЉЃЌЕуNЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЁЂЕуCЃЈ0ЃЌ4ЃЉЃЌ
ЃЉЁЂЕуCЃЈ0ЃЌ4ЃЉЃЌ
дђжБЯпCNБэДяЪНжаЕФkЮЊЉ![]() ЃЌЩшЕуMЯђЯТЦНвЦ4mИіЕЅЮЛЃЌдђЯђгвЦНвЦ3mИіЕЅЮЛЃЌ
ЃЌЩшЕуMЯђЯТЦНвЦ4mИіЕЅЮЛЃЌдђЯђгвЦНвЦ3mИіЕЅЮЛЃЌ
ЙЪЕуMЁфЃЈ3mЃЌ![]() Љ4mЃЉЃЌ
Љ4mЃЉЃЌ
дђMMЁф2ЃНЃЈ3mЃЉ2+ЃЈ4mЃЉ2ЃН25m2ЃЛOM2ЃНЃЈ![]() ЃЉ2ЃЛOMЁф2ЃНЃЈ3mЃЉ2+ЃЈ
ЃЉ2ЃЛOMЁф2ЃНЃЈ3mЃЉ2+ЃЈ![]() Љ4mЃЉ2ЃЛ
Љ4mЃЉ2ЃЛ
ЂйЕБMMЁфЃНOMЪБЃЌ25m2ЃНЃЈ![]() ЃЉ2ЃЌНтЕУЃКmЃН
ЃЉ2ЃЌНтЕУЃКmЃН![]() ЃЛ
ЃЛ
ЂкЕБMMЁфЃНOMЁфЪБЃЌЭЌРэПЩЕУЃКmЃН![]() ,ЁрMЁфЃЈ
,ЁрMЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЂлЕБOMЁфЃНOMЪБЃЌЭЌРэПЩЕУЃКmЃН![]() ЃЌЁрMЁфЃЈ
ЃЌЁрMЁфЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
злЩЯЃЌЕуMЁфЕФзјБъЮЊЃКЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ

 КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ
КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ
ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИЁОЬтФПЁПжиЧьЃЌБ№ГЦЁАЩНГЧЁБЁЂЁАЮэЖМЁБЃЌТУгЮзЪдДЗсИЛЃЌздШЛШЫЮФТУгЮОАЕуЖРОпЬиЕуЃЎНќФъРДЃЌжиЧьвдЦфЖРЬиЁА3DФЇЛУЁБАуЕФГЧЪаїШСІЮќв§СЫжкЖрКЃФкЭтгЮПЭЃЌГЩЮЊУћИБЦфЪЕЕФТУгЮДђПЈЭјКьГЧЪаЃЎФГжабЇЯыСЫНтИУаЃОХФъМЖ1200УћбЇЩњЖджиЧьздШЛШЫЮФТУгЮОАЕуЕФСЫНтЧщПіЃЌДгОХЃЈ1ЃЉЁЂОХЃЈ2ЃЉАрЗжБ№ГщШЁСЫ30УћЭЌбЇНјааВтЪдЃЌЛёЕУСЫЫћУЧЕФГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааећРэЁЂУшЪіКЭЗжЮіЃЎЯТУцИјГіСЫВПЗжаХЯЂЃК
aЃЎВтЪдГЩМЈЗжГЩ5зщЃЌЦфжаAзщЃК50ЃМxЁм60ЃЌBзщЃК60ЃМxЁм70ЃЌCзщЃК70ЃМxЁм80ЃЌDзщЃК80ЃМxЁм90ЃЌEзщЃК90ЃМxЁм100ЃЎВтЪдГЩМЈЭГМЦЭМШчЯТЃК
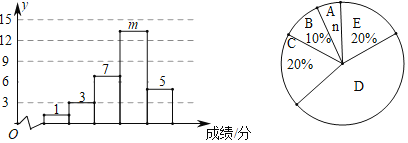
bЃЎОХЃЈ2ЃЉАрDзщЕФВтЪдГЩМЈЗжБ№ЪЧЃК81ЁЂ82ЁЂ82ЁЂ83ЁЂ84ЁЂ85ЁЂ86ЁЂ87ЁЂ88ЁЂ89ЁЂ89ЁЂ90ЁЂ90ЁЂ90ЃЎ
cЃЎОХЃЈ1ЃЉЃЈ2ЃЉАрВтЪдГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
ПЮГЬ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ |
ОХЃЈ1ЃЉ | 84.2 | 84 | 89 |
ОХЃЈ2ЃЉ | 84.6 | Іа | 90 |
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉИљОнЬтвтЃЌжБНгаДГіmЃЌnЕФжЕЃКmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЛОХЃЈ2ЃЉАрВтЪдГЩМЈЩШаЮЭГМЦЭМжаAзщЕФдВаФНЧІСЃНЁЁ ЁЁЁуЃЛ
ЃЈ2ЃЉдкДЫДЮВтЪджаЃЌФуШЯЮЊЁЁ ЁЁАрЕФбЇЩњЖджиЧьздШЛШЫЮФОАЕуИќСЫНтЃЈЬюЁАОХЃЈ1ЃЉЁБЛђЁАОХЃЈ2ЃЉЁБЃЉЃЌЧыЫЕУїРэгЩЃЈвЛЬѕРэгЩМДПЩЃЉЃКЁЁ ЁЁЃЛ
ЃЈ3ЃЉМйЩшИУаЃОХФъМЖбЇЩњЖМВЮМгДЫДЮВтЪдЃЌВтЪдГЩМЈДѓгк90ЗжЮЊгХауЃЌЧыЙРМЦИУаЃОХФъМЖЖджиЧьздШЛШЫЮФОАЕуЕФСЫНтДяЕНгХауЕФШЫЪ§ЃЎ