题目内容
 (2012•百色)如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.
(2012•百色)如图,在平面直角坐标系中,抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0).直线y=h(h为常数,且0<h<6)与BC交于点D,与y轴交于点E,与AC交于点F,与抛物线在第二象限交于点G.(1)求抛物线的解析式;
(2)连接BE,求h为何值时,△BDE的面积最大;
(3)已知一定点M(-2,0).问:是否存在这样的直线y=h,使△OMF是等腰三角形?若存在,请求出h的值和点G的坐标;若不存在,请说明理由.
分析:(1)由抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),利用待定系数法即可求得抛物线的解析式;
(2)首先利用待定系数法求得经过点B和点C的直线的解析式,由题意可得点E的坐标为(0,h),则可求得点D的坐标为(
,h),则可得S△BDE=
•OE•DE=
•h•
=-
(h-3)2+
,然后由二次函数的性质,即可求得△BDE的面积最大;
(3)分别从①若OF=OM,则
=2、②若OF=MF,则
=
与③若MF=OM,则
=
去分析求解即可求得答案.
(2)首先利用待定系数法求得经过点B和点C的直线的解析式,由题意可得点E的坐标为(0,h),则可求得点D的坐标为(
| 6-h |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6-h |
| 3 |
| 1 |
| 6 |
| 3 |
| 2 |
(3)分别从①若OF=OM,则
(
|
(
|
(
|
(
|
(
|
解答:解:(1)∵抛物线y=ax2+bx+6经过点A(-3,0)和点B(2,0),
∴
.
解得:
.
∴抛物线的解析式为y=-x2-x+6.
(2)∵把x=0代入y=-x2-x+6,得y=6.
∴点C的坐标为(0,6).
设经过点B和点C的直线的解析式为y=mx+n,则
,
解得
.
∴经过点B和点C的直线的解析式为:y=-3x+6.
∵点E在直线y=h上,
∴点E的坐标为(0,h).
∴OE=h.
∵点D在直线y=h上,
∴点D的纵坐标为h.
把y=h代入y=-3x+6,得h=-3x+6.
解得x=
.
∴点D的坐标为(
,h).
∴DE=
.
∴S△BDE=
•OE•DE=
•h•
=-
(h-3)2+
.
∵-
<0且0<h<6,
∴当h=3时,△BDE的面积最大,最大面积是
.
(3)存在符合题意的直线y=h.
设经过点A和点C的直线的解析式为y=kx+p,则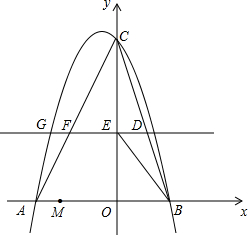
,
解得
.
故经过点A和点C的直线的解析式为y=2x+6.
把y=h代入y=2x+6,得h=2x+6.
解得x=
.
∴点F的坐标为(
,h).
在△OFM中,OM=2,OF=
,MF=
.
①若OF=OM,则
=2,
整理,得5h2-12h+20=0.
∵△=(-12)2-4×5×20=-256<0,
∴此方程无解.
∴OF=OM不成立.
②若OF=MF,则
=
,
解得h=4.
把y=h=4代入y=-x2-x+6,得-x2-x+6=4,
解得x1=-2,x2=1.
∵点G在第二象限,
∴点G的坐标为(-2,4).
③若MF=OM,则
=2,
解得h1=2,h2=-
(不合题意,舍去).
把y=h1=2代入y=-x2-x+6,得-x2-x+6=2.
解得x1=
,x2=
.
∵点G在第二象限,
∴点G的坐标为(
,2).
综上所述,存在这样的直线y=2或y=4,使△OMF是等腰三角形,当h=4时,点G的坐标为(-2,4);当h=2时,点G的坐标为(
,2).
∴
|
解得:
|
∴抛物线的解析式为y=-x2-x+6.
(2)∵把x=0代入y=-x2-x+6,得y=6.
∴点C的坐标为(0,6).
设经过点B和点C的直线的解析式为y=mx+n,则
|
解得
|
∴经过点B和点C的直线的解析式为:y=-3x+6.
∵点E在直线y=h上,
∴点E的坐标为(0,h).
∴OE=h.
∵点D在直线y=h上,
∴点D的纵坐标为h.
把y=h代入y=-3x+6,得h=-3x+6.
解得x=
| 6-h |
| 3 |
∴点D的坐标为(
| 6-h |
| 3 |
∴DE=
| 6-h |
| 3 |
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 6-h |
| 3 |
| 1 |
| 6 |
| 3 |
| 2 |
∵-
| 1 |
| 6 |
∴当h=3时,△BDE的面积最大,最大面积是
| 3 |
| 2 |
(3)存在符合题意的直线y=h.
设经过点A和点C的直线的解析式为y=kx+p,则

|
解得
|
故经过点A和点C的直线的解析式为y=2x+6.
把y=h代入y=2x+6,得h=2x+6.
解得x=
| h-6 |
| 2 |
∴点F的坐标为(
| h-6 |
| 2 |
在△OFM中,OM=2,OF=
(
|
(
|
①若OF=OM,则
(
|
整理,得5h2-12h+20=0.
∵△=(-12)2-4×5×20=-256<0,
∴此方程无解.
∴OF=OM不成立.
②若OF=MF,则
(
|
(
|
解得h=4.
把y=h=4代入y=-x2-x+6,得-x2-x+6=4,
解得x1=-2,x2=1.
∵点G在第二象限,
∴点G的坐标为(-2,4).
③若MF=OM,则
(
|
解得h1=2,h2=-
| 6 |
| 5 |
把y=h1=2代入y=-x2-x+6,得-x2-x+6=2.
解得x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∵点G在第二象限,
∴点G的坐标为(
-1-
| ||
| 2 |
综上所述,存在这样的直线y=2或y=4,使△OMF是等腰三角形,当h=4时,点G的坐标为(-2,4);当h=2时,点G的坐标为(
-1-
| ||
| 2 |
点评:此题考查了待定系数法求函数的解析式、二次函数的性质以及等腰三角形的性质.此题难度较大,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 (2012•百色)如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA=
(2012•百色)如图,Rt△OA1B1是由Rt△OAB绕点O顺时针方向旋转得到的,且A、O、B1三点共线.如果∠OAB=90°,∠AOB=30°,OA= (2012•百色)如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( )
(2012•百色)如图,在矩形ABCD中,AB=6cm,BC=4cm.动点E从点B出发,沿着线路BC→CD→DA运动,在BC段的平均速度是1cm/s,在CD段的平均速度是2cm/s,在DA段的平均速度是4cm/s,到点A停止.设△ABE的面积为y(cm2),则y与点E的运动时间t(s)的函数关系图象大致是( ) (2012•百色)如图,在平面直角坐标系中,等腰梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上,且A(-4,0),B(6,0),D(0,3).
(2012•百色)如图,在平面直角坐标系中,等腰梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上,且A(-4,0),B(6,0),D(0,3). (2012•百色)如图,△ABC内接于⊙O,AB是直径,直线l是经过点C的切线,BD⊥l,垂足为D,且AC=8,sin∠ABC=
(2012•百色)如图,△ABC内接于⊙O,AB是直径,直线l是经过点C的切线,BD⊥l,垂足为D,且AC=8,sin∠ABC=