题目内容
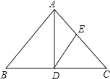
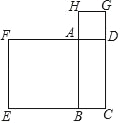
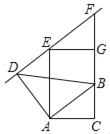
【题目】如图,在正方形![]() 中,边长为2的等边三角形
中,边长为2的等边三角形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上,则正方形
上,则正方形![]() 的面积等于_________.
的面积等于_________.

【答案】![]()
【解析】
首先根据四边形![]() 是正方形得出AB=AD,∠B=∠D=90°,根据△AEF是等边三角形得出AE=AF,最后根据HL即可证明△ABE≌△ADF;根据全等的性质:CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设
是正方形得出AB=AD,∠B=∠D=90°,根据△AEF是等边三角形得出AE=AF,最后根据HL即可证明△ABE≌△ADF;根据全等的性质:CE=CF,∠C=90°,从而得出△ECF是等腰直角三角形,再根据勾股定理得出EC的值,设![]() ,则
,则![]() ,在Rt△ABE中,
,在Rt△ABE中,![]() ,求出
,求出![]() 的值,即可得出正方形
的值,即可得出正方形![]() 的边长,最后求出正方形
的边长,最后求出正方形![]() 的面积.
的面积.
解:∵四边形![]() 是正方形,∴AB=AD,∠B=∠D=90°,
是正方形,∴AB=AD,∠B=∠D=90°,
∵△AEF是等边三角形,∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴CE=CF,∠C=90°,
即△ECF是等腰直角三角形,
由勾股定理得![]() ,
,
∴![]() ,
,
在Rt△ABE中,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
∴![]() ,
,
∴![]() ,
,
故答案为![]() .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目