题目内容
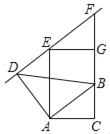
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求证:AD⊥EF;
(2)求CG的长.
【答案】(1)证明见解析;(2)CG= 12.5.
【解析】
(1)由平移的性质可知:AB∥DF,再利用平行线的性质即可证明;
(2)先判断出∠ADE=∠ACB,进而得出△ADE∽△ACB,得出比例式求出AE,即可得出结论.
(1)∵线段AD是由线段AB绕点A按逆时针方向旋转90°得到,
∴∠DAB=90°,
∵△EFG是△ABC沿CB方向平移得到,
∴AB∥EF,
∴∠ADF+∠DAB=180°,
∴∠ADF=90°,
∴AD⊥EF;
(2)由平移的性质得,AE∥CG,AB∥EF,
∴∠DEA=∠DFC=∠ABC,∠ADE+∠DAB=180°,
∵∠DAB=90°,
∴∠ADE=90°,
∵∠ACB=90°,
∴∠ADE=∠ACB,
∴△ADE∽△ACB,
∴![]() =
=![]() ,
,
∵AC=8,AB=AD=10,
∴AE=12.5,
由平移的性质得,CG=AE=12.5.

练习册系列答案
相关题目