Question

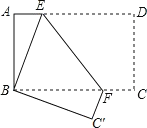
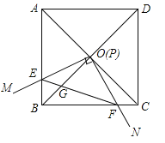
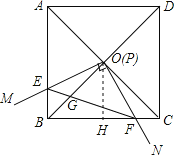
【题目】已知：如图，四边形ABCD是边长为1的正方形，对角线AC、BD相交于点O．过点O作一直角∠MON，直角边OM、ON分别与OA、OB重合，然后逆时针旋转∠MON，旋转角为θ（0°＜θ＜90°），OM、ON分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是________(填序号)．

①；②S四边形OEBF：S正方形ABCD=1：2；③；④OGBD=AE2+CF2；⑤在旋转过程中，当△BEF与△COF的面积之和最大时，．

Answer 1

【答案】①③④

【解析】

①②③证明△BOE≌△COF，结合正方形的性质可判断；④证明，结合△BOE≌△COF的性质即可证得；⑤作OH⊥BC，表示出S△BEF+S△COF，即可判断．

①∵四边形ABCD是正方形，

∴OB=OC，∠OBE=∠OCF=45°，∠BOC=90°，

∴∠BOF+∠COF=90°，

∵∠EOF=90°，

∴∠BOF+∠COE=90°，

∴∠BOE=∠COF，

在△BOE和△COF中，

，

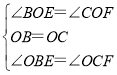∴△BOE≌△COF（ASA），

∴OE=OF，BE=CF，

∴EF=OE；故①正确；

②∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=S正方形ABCD，

∴S四边形OEBF：S正方形ABCD=1：4；故②错误；

③∴BE+BF=BF+CF=BC=OA；故③正确；

④∵

∴

∴

∴

∵

∴

∵在中，

∴

∴，故④正确；

⑤过点O作OH⊥BC，

∵BC=1，

∴OH=BC=，

设AE=，则BE=CF=1-，BF=，

∴S△BEF+S△COF=BEBF+CFOH=（1-）+（1-）×=-（-）2+，

∵＜0，

∴当=时，S△BEF+S△COF最大；

即在旋转过程中，当△BEF与△COF的面积之和最大时，AE=；故⑤错误；

故答案为①③④．