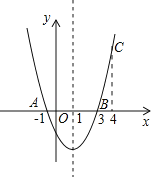题目内容
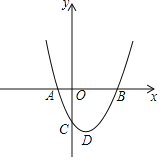
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 上,
上,![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() ,
,![]() 、
、![]() 的长是方程
的长是方程![]() 的两个实数根,且
的两个实数根,且![]() ,点
,点![]() 是线段
是线段![]() 延长线上的一个动点,
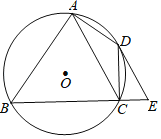
延长线上的一个动点,![]() 的外接圆
的外接圆![]() 与
与![]() 轴的另一个交点是
轴的另一个交点是![]() .
.
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)求反比例函数的解析式;
(3)连接![]() 求
求![]() 的值.
的值.
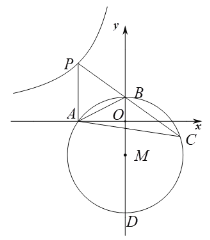
【答案】(1)点A坐标为(-6,0),点B坐标为(0,2);(2)反比例函数解析式为:![]() ;(3)
;(3)![]() .
.
【解析】
(1)先解一元二次方程求出线段长,再转化为坐标即可;
(2)设出点P坐标,根据PA=PB建立方程求解即可;
(3)连接AM,设半径为r,在Rt△AOM中利用勾股定理求出半径长,再过点P作PH⊥y轴,根据线段之间的关系得到HM的长度,在Rt△PMH中即可求出结果.
解:(1)![]() ,解得:
,解得:![]() 或
或![]() ,
,
∵OA,OB的长是方程![]() 的两个实数根,且OA>OB,
的两个实数根,且OA>OB,
∴OA=6,OB=2,
∴点A坐标为(-6,0),点B坐标为(0,2);
(2)设点![]() ,由
,由![]() 知
知![]() ,
,
∴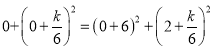 ,
,
解得:![]() ,
,
∴点P(-6,10),反比例函数解析式为:![]() ;
;
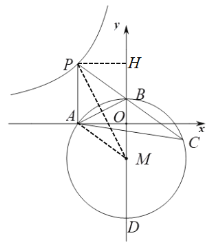
(3)连接AM,设半径为r,则OM=r-2,
∵在![]() 中,
中,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴BM=AM=10,
过点P作PH⊥y轴,则OH =10,PH=6,
∴HB=OH-OB=8,
∴HM=HB+BM=18,
∴在![]() 中,
中,![]() .
.

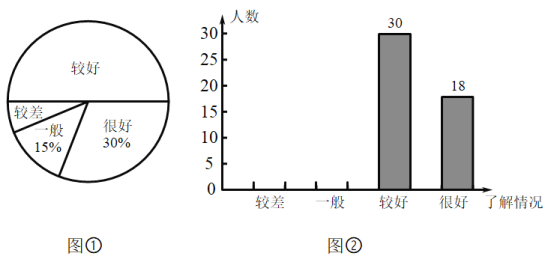
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸在176~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下.
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据

分析数据
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
(1)求![]() ,
,![]() 的值;
的值;
(2)计算甲车间样品的合格率;
(3)估计乙车间生产的1000个该款新产品中合格产品有多少个;
(4)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.