题目内容
【题目】如图，已知在Rt△ABC中，∠ABC=90°，点D沿BC自B向C运动（点D与点B、C不重合），作BE⊥AD于E，CF⊥AD于F，则BE+CF的值（ ）
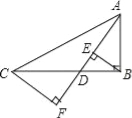
A．不变 B．增大 C．减小 D．先变大再变小
【答案】C．
【解析】
试题分析：已知BE⊥AD于E，CF⊥AD于F，可得CF∥BE，根据平行线的性质得∠DCF=∠DBF，设CD=a，DB=b，∠DCF=∠DEB=α，所以CF=DCcosα，BE=DBcosα，即可得BE+CF=（DB+DC）cosα=BCcosα，因∠ABC=90°，所以O＜α＜90°，当点D从B→D运动时，α是逐渐增大的，cosα的值是逐渐减小的，所以BE+CF=BCcosα的值是逐渐减小的．故答案选C．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】在2016CCTV英语风采大赛中，娄底市参赛选手表现突出，成绩均不低于60分．为了更好地了解娄底赛区的成绩分布情况，随机抽取利了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，得到如图的两幅不完整的统计图表：
根据所给信息，解答下列问题：
（1）在表中的频数分布表中，m= ，n= ．
成绩 | 频数 | 频率 |
60≤x＜70 | 60 | 0.30 |
70≤x＜80 | m | 0.40 |
80≤x＜90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
（2）请补全图中的频数分布直方图．
（3）按规定，成绩在80分以上（包括80分）的选手进入决赛．若娄底市共有4000人参数，请估计约有多少人进入决赛？