题目内容
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x﹣2)2+k经过点A、B.求:

(1)点A、B的坐标;
(2)抛物线的函数表达式;
(3)若点M是该抛物线对称轴上的一点,求AM+BM的最小值及点M的坐标;
(4)在抛物线对称轴上是否存在点P,使得以A、B、P为顶点的三角形为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
【答案】(1)点A的坐标为(1,0).点B的坐标为(0,3).(2)y=x2﹣4x+3.(3)M(2,1).(4)点P的坐标为(2,2)或(2,3)或(2,3+![]() )或(2,3﹣
)或(2,3﹣![]() ).
).
【解析】
试题分析:(1)将x=0代入直线的解析式可求得点B的坐标,将y=0代入直线的解析式可求得点A的坐标;
(2)将点A、B的坐标代入抛物线的解析式得到关于a、k的方程组,求得a、k的值,从而可求得抛物线的解析式;
(3)先求得抛物线的对称轴方程,从而可求得点C的坐标,由轴对称图形的性质可知AM+BM=BM+MC,当点B、M、C在一条直线上时,AM+BM有最小值,在Rt△BOC中,由勾股定理可求得BC的长,从而得到AM+BM的最小值,然后由△CDM∽△COB,可求得DM=1,从而得到点M的坐标;
(4)设点P的坐标为(2,m),然后分为AP=PB,AP=AB,BA=BP三种情况列方程求解即可.
解:(1)∵将x=0代入直线的解析式得:y=3,
∴点B的坐标为(0,3).
∵将y=0代入直线的解析式得:﹣3x+3=0,解得:x=1.
∴点A的坐标为(1,0).
(2)将A(1,0)、B(0,3)代入抛物线的解析式得:![]() ,
,
解得:a=1,k=﹣1.
抛物线的解析式为y=x2﹣4x+3.
(3)如图所示:连接BC交抛物线的对称轴于点M,连接AM.
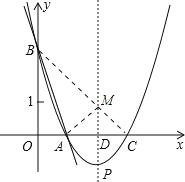
∵由题意可知抛物线的对称轴为x=2,
∴点C的坐标为(3,0).
∵点A与点M关于x=2对称,
∴AN=MC.
∴AM+BM=BM+MC.
∵当点B、M、C在一条直线上时,AM+BM有最小值,AM+BM的最小值为BC的长.
∴AM+BM的最小值=![]() =3
=3![]() .
.
∵MD∥OB,
∴△CDM∽△COB.
∴![]() ,即
,即![]() .
.
解得:MD=1.
∴M(2,1).
(4)设点P的坐标为(2,m).
①当PA=PB时,由两点间的距离公式可知:(2﹣1)2+(m﹣0)2=(2﹣0)2+(m﹣3)2.
整理得:6m=12.
解得:m=2.
点P的坐标为(2,2).
②当AP=AB时,由两点间的距离公式可知:(2﹣1)2+(m﹣0)2=(1﹣0)2+(0﹣3)2.
整理得:m2=9.
解得:m=3或m=﹣3(舍去).
点P的坐标为(2,3).
③当BA=BP时,由两点间的距离公式可知:(1﹣0)2+(0﹣3)2=(2﹣0)2+(m﹣3)2.
整理得:(m﹣3)2=6.
解得:m=3+![]() 或m=3﹣
或m=3﹣![]() .
.
点P的坐标为(2,3+![]() )或(2,3﹣
)或(2,3﹣![]() ).
).
综上所述,点P的坐标为(2,2)或(2,3)或(2,3+![]() )或(2,3﹣
)或(2,3﹣![]() ).
).
