Question

【题目】已知：如图，在平面直角坐标系xOy中，一次函数y=-x的图象与反比例函数y=的图象交于A、B两点．

（1）求k的值；

（2）如果点P在y轴上，且满足以点A、B、P为顶点的三角形是直角三角形，直接写出点P的坐标．

Answer 1

【答案】（1）-1；（2）P点坐标为（0，）、（0，-）、（0，2）、（0，-2）．

【解析】

试题分析：（1）首先求出A点坐标，再把A点坐标代入y=即可得到k的值；

（2）BD⊥y轴，AC⊥y轴，如图，设P点坐标为（0，y），先根据对称得到B点坐标为（1，-1），再根据勾股定理得到AB2=22+22=8，PB2=PD2+BD2=（y+1）2+12，PA2=PC2+AC2=（y-1）2+12，然后分类讨论：当△APB是以AB为斜边的直角三角形，则PB2+PA2=AB2；当△APB是以PB为斜边的直角三角形，则AB2+PA2=PB2；当△APB是以PA为斜边的直角三角形，AB2+PB2=PA2，分别得到关于y的方程，解方程求出y的值即可得到P点坐标．

试题解析：（1）∵一次函数y=-x的图象与反比例函数y=的图象交于A、B两点，

根据图象可得出A点横坐标为-1，代入一次函数解析式，

∴y=-（-1）=1，

∴A点坐标为：（-1，1），

∵反比例函数y=的图象经过点A（-1，1），

∴k=-1×1=-1；

（2）作BD⊥y轴，AC⊥y轴，如图，设P点坐标为（0，y），

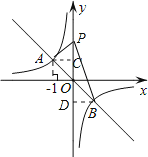
∵点A与B点关于原点对称，

∴B点坐标为（1，-1），

∴AB2=22+22=8，PB2=PD2+BD2=（y+1）2+12，PA2=PC2+AC2=（y-1）2+12，

分类：当△APB是以AB为斜边的直角三角形，则PB2+PA2=AB2，

∴PB2+PA2=AB2，即（y+1）2+12+（y-1）2+12=8，解得y=±；

当△APB是以PB为斜边的直角三角形，

∴AB2+PA2=PB2，即（y+1）2+12=（y-1）2+12+8，解得y=2；

当△APB是以PA为斜边的直角三角形，

∴AB2+PB2=PA2，即（y-1）2+12=（y+1）2+12+8，解得y=-2；

∴P点坐标为（0，）、（0，-）、（0，2）、（0，-2）．