题目内容
【题目】已知菱形ABCD中,AB=4,∠BAD=120°,点P是直线AB上任意一点,连接PC,在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30°.
(1)如图,当点P在边AB上,且BP=3时,求PC的长;
(2)当点P在射线BA上,且BP=n(0≤n<8)时,求QC的长;(用含n的式子表示)
(3)连接PQ,直线PQ与直线BC相交于点E,如果△QCE与△BCP相似,请直接写出线段BP的长.
【答案】(1)![]() ;(2)QC=
;(2)QC=![]() (0≤n<8);(3)BP的值为2+2
(0≤n<8);(3)BP的值为2+2![]() 或2
或2![]() ﹣2.
﹣2.
【解析】
(1)如图1中,作PH⊥BC于H.解直角三角形求出BH,PH,在Rt△PCH中,由勾股定理即可得出答案.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.证明△POQ∽△BOC,推出∠OPQ=∠OBC=30°=∠PCQ,推出PQ=CQ,推出PC=![]() CQ,在Rt△PHB中,BH=
CQ,在Rt△PHB中,BH=![]() n,PH=
n,PH=![]() n,根据PC2=PH2+CH2,可得结论.
n,根据PC2=PH2+CH2,可得结论.
(3)分三种情形:①如图2中,若直线QP交直线BC于B点左侧的点E.②如图3中,若直线QP交直线BC于C点右侧的点E.③如图4中,当点P在AB的延长线上时,由相似三角形的性质分别求解即可.
解:(1)如图1中,作PH⊥BC于H.
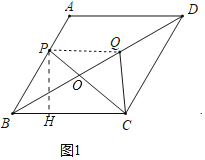
∵四边形ABCD是菱形,
∴AB=BC=4,AD∥BC,
∴∠A+∠ABC=180°,
∵∠A=120°,
∴∠PBH=60°,
∵PB=3,∠PHB=90°,
∴BH=PBcos60°=![]() ,PH=PBsin60°=
,PH=PBsin60°=![]() ,
,
∴CH=BC﹣BH=4﹣![]() =
=![]() ,
,
∴PC═![]() =
=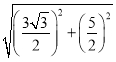 =
=![]() .
.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵四边形ABCD是菱形,
∴∠ABD=
∵∠PCQ=30°,
∴∠PBO=∠QCO,
∵∠POB=∠QOC,
∴△POB∽△QOC,
∴![]() ,
,
∴![]() ,
,
∵∠POQ=∠BOC,
∴△POQ∽△BOC,
∴∠OPQ=∠OBC=30°=∠PCQ,
∴PQ=QC,
∴PC=![]() QC,
QC,
在Rt△PHB中,BP=n,
∴BH=![]() n,PH=
n,PH=![]() n,
n,
∵PC2=PH2+CH2,
∴3QC2=(![]() n)2+(4﹣
n)2+(4﹣![]() n)2,
n)2,
∴QC=![]() (0≤n<8).
(0≤n<8).
(3)①如图2中,若直线QP交直线BC于B点左侧的点E.
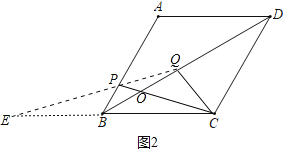
此时∠CQE=120°,
∵∠PBC=60°,
∴△PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于点C右侧的点E.
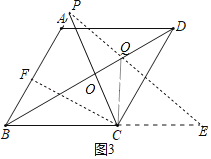
则∠CQE=∠B=QBC+∠QCP=60°=∠CBP,
∵∠PCB>∠E,
∴只可能∠BCP=∠QCE=75°,
作CF⊥AB于F,则BF=2,CF=2![]() ,∠PCF=45°,
,∠PCF=45°,
∴PF=CF=2![]() ,
,
此时BP=2+2![]() ,
,
③如图4中,当点P在AB的延长线上时,
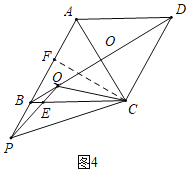
∵△CBE与△CBP相似,
∴∠CQE=∠CBP=120°,
∴∠QCE=∠CBP=15°,
作CF⊥AB于F.
∵∠FCB=30°,
∴∠FCB=45°,
∴BF=![]() BC=2,CF=PF=2
BC=2,CF=PF=2![]() ,
,
∴BP=2![]() ﹣2.
﹣2.
综上所述,满足条件的BP的值为2+2![]() 或2
或2![]() ﹣2.
﹣2.