题目内容
【题目】 完成下面的证明.
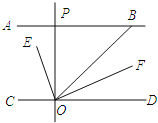
如图,已知AB∥CD∥EF, 写出∠A,∠C,∠AFC的关系并说明理由.
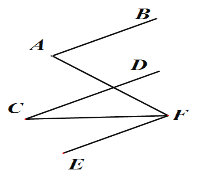
解:∠AFC= . 理由如下:
∵AB∥EF(已知),
∴∠A= (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ( ).
∵∠AFC= - ,
∴∠AFC= (等量代换).
【答案】∠A—∠C; ∠AFE, 两直线平行,内错角相等; ∠CFE, 两直线平行,内错角相等; ∠AFE, ∠CFE;∠A—∠C ,等量代换.
【解析】
根据平行线的性质得∠A=∠AFE,∠C=∠CFE,在利用角的和差即可得出答案.
解:∠AFC= ∠A—∠C 理由如下:
∵AB∥EF(已知),
∴∠A= ∠AFE (两直线平行,内错角相等).
∵CD∥EF(已知),
∴∠C= ∠CFE ( 两直线平行,内错角相等).
∵∠AFC= ∠AFE - ∠CFE
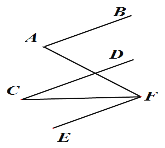
∴∠AFC= ∠A—∠C (等量代换).

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目