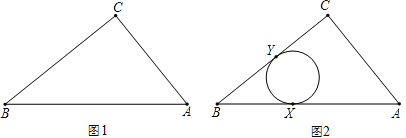题目内容
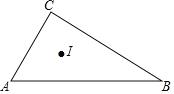
【题目】已知∠ACB=90°,∠CAB=a,且sina=![]() ,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
,I为内心,则△ABC的内切圆半径r与△BIC的外接圆半径R之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作ID⊥AC于D,△CIB外接圆的圆心为O,作OE⊥BC于E,交直线ID于F,连接OC,求出直角三角形ABC的内切圆半径,由勾股定理得出方程,求出△BIC的外接圆半径R,即可得出结果.
作ID⊥AC于D,△CIB外接圆的圆心为O,作OE⊥BC于E,交直线ID于F,连接OC,如图所示:
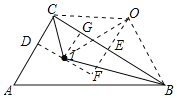
∵∠ACB=90°,∠CAB=a,且sina=![]() ,
,
设AB=5b,BC=4b,则AC=3b,
∴△ABC的内切圆的半径![]() ,
,
∵I是Rt△ABC的内心,
∴CD=ID=CG=b,
∵OE⊥BC,
∴CE=BE=![]() BC=2b,
BC=2b,
易得四边形CDFE为矩形,
∴EF=CD=b,DF=CE=2b,
∴IF=2b-b=b,
设OE=x,⊙O的半径为R,则OF=x+b,OC=OI=R,
在Rt△OCE中,x![]() +(2b)
+(2b)![]() =R
=R![]() ①,
①,
在Rt△OIF中,(x+b)![]() +b
+b![]() =R
=R![]() ②,
②,
②-①得:2ax=2a![]() ,解得x=a,
,解得x=a,
∴![]()
∴△ABC的内切圆半径r与△BIC的外接圆半径R之比=![]() ;
;
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目