题目内容
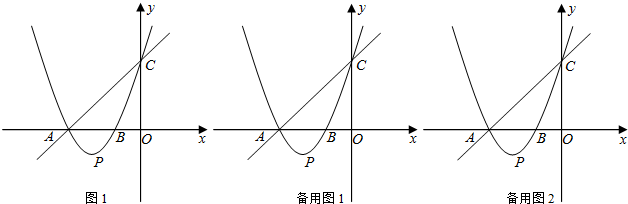
如图1，直线y=x+3与x轴、y轴分别交于点A、点C，经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B，顶点P的横坐标为-2．
（1）求该抛物线的解析式；
（2）连接BC，得△ABC．若点D在x轴上，且以点P、B、D为顶点的三角形与△ABC相似，求出点P的坐标并直接写出此时△PBD外接圆的半径；
（3）设直线l：y=x+t，若在直线l上总存在两个不同的点E，使得∠AEB为直角，则t的取值范围是
（4）点F是抛物线上一动点，若∠AFC为直角，则点F坐标为
（1）求该抛物线的解析式；
（2）连接BC，得△ABC．若点D在x轴上，且以点P、B、D为顶点的三角形与△ABC相似，求出点P的坐标并直接写出此时△PBD外接圆的半径；
（3）设直线l：y=x+t，若在直线l上总存在两个不同的点E，使得∠AEB为直角，则t的取值范围是
2-
＜t＜2+
，且t≠1、t≠3
| 2 |
| 2 |
2-
＜t＜2+
，且t≠1、t≠3
；| 2 |
| 2 |
（4）点F是抛物线上一动点，若∠AFC为直角，则点F坐标为
（
，
）或（
，
）
-5+
| ||
| 2 |
1-
| ||
| 2 |
-5-
| ||
| 2 |
1+
| ||
| 2 |
（
，
）或（
，
）
．-5+
| ||
| 2 |
1-
| ||
| 2 |
-5-
| ||
| 2 |
1+
| ||
| 2 |
分析：（1）知道了抛物线顶点P的横坐标，那么也就知道了抛物线的对称轴方程，点A、C的坐标可由直线AC求得，而点A、B关于抛物线对称轴对称，所以点B的坐标可得，再由待定系数法确定抛物线的解析式．
（2）由A、P、B、C四点坐标不难看出：∠PBA=∠CAB=45°，那么若以点P、B、D为顶点的三角形与△ABC相似，只需找出另一组对应角相等即可，分两种情况讨论：①∠PCB=∠ABC，②∠BPC=∠ABC；在上述两种情况中，先设出点D的坐标，再表示出BD、BP、AB、AC的长，根据得到的不同比例线段，列式求出点D的坐标．知道了PD的长，由2r=
求出三角形的外接圆半径．
（3）∠AEB是直角，那么点E必为以AB为直径的圆与直线l的交点，若符合条件的点E有两个，那么直线l与以AB为直角的圆有两个交点，所以在判断t的取值范围时，考虑两个方面：①先求出最大、最小值，此时直线l与以AB为直角的圆相切；②∠AEB是直角，那么点A、E或点B、E不重合，即直线l不能经过点A、B．
（4）过点F作y轴的垂线FH，过点F作x轴的垂线FG，先证明△AFG∽△CFH，根据得到比例线段列式求出点F的坐标．
（2）由A、P、B、C四点坐标不难看出：∠PBA=∠CAB=45°，那么若以点P、B、D为顶点的三角形与△ABC相似，只需找出另一组对应角相等即可，分两种情况讨论：①∠PCB=∠ABC，②∠BPC=∠ABC；在上述两种情况中，先设出点D的坐标，再表示出BD、BP、AB、AC的长，根据得到的不同比例线段，列式求出点D的坐标．知道了PD的长，由2r=
| PD |
| sin∠PBD |
（3）∠AEB是直角，那么点E必为以AB为直径的圆与直线l的交点，若符合条件的点E有两个，那么直线l与以AB为直角的圆有两个交点，所以在判断t的取值范围时，考虑两个方面：①先求出最大、最小值，此时直线l与以AB为直角的圆相切；②∠AEB是直角，那么点A、E或点B、E不重合，即直线l不能经过点A、B．
（4）过点F作y轴的垂线FH，过点F作x轴的垂线FG，先证明△AFG∽△CFH，根据得到比例线段列式求出点F的坐标．
解答：解：（1）由直线y=x+3知，点A（-3，0）、C（0，3）；
抛物线的顶点P的横坐标为-2，所以对称轴x=-2，则 B（-1，0）；
将点A、B、C的坐标代入抛物线的解析式中，得：
，
解得
故抛物线的解析式：y=x2+4x+3．
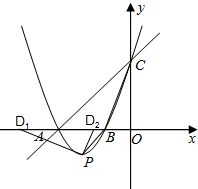（2）由（1）的抛物线解析式知：y=x2+4x+3=（x+2）2-1，
则顶点P（-2，-1）；
已知A（-3，0）、C（0，3），B（-1，0）、P（-2，-1）知：∠CAB=∠PBA=45°，AB=2、AC=3
、BP=
；
①当∠ABC=∠BPD1时，△ABC∽△BPD1，得：
=
，即
=
，BD1=3；
则D1（-4，0），则 PD1=
；
故△PBD外接圆半径 r1=
=
=
=
；
②当∠ABC=∠BD2P时，△ABC∽△BD2P，得：
=
，即
=
，BD2=
；
则D2（-
，0），则 PD2=
；
故△PBD外接圆半径 r2=
=
=
=
；
综上，有两组解分别是：①P（-2，-1），D1（-4，0），r1=
；②P（-2，-1），D2（-
，0），r2=
．
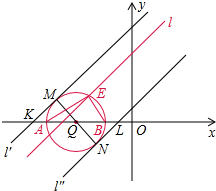（3）若∠AEB为直角，那么点E在以AB为直径的⊙Q上，那么点E为直线l与⊙Q的交点（如右图）；
取与直线l平行，且与⊙Q相切的直线l′、l″，如右图，设切点分别为M、N；
∵直线l∥直线l′∥直线l″，且它们的斜率k=1，
∴∠MKQ=∠NQL=45°．
Rt△KMQ中，QM=
AB=1，∠MKQ=45°，则 KQ=
，
同理可得 QL=
；
∴K（-2-
，0）、L（-2+
，0）；
若直线l与⊙Q始终有两个交点，那么直线l必在直线l′、l″之间，由于直线l与x轴交点为（-t，0），有：
-2-
＜-t＜-2+
，即 2-
＜t＜2+
；
而∠AEB是直角，那么点A与点E以及点B与点E都不重合，即直线l不经过点A、B，所以，-t≠-1，且-t≠-3；
综上，t的取值范围：2-
＜t＜2+
，且t≠1、t≠3．
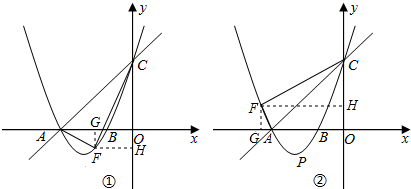（4）设点F（x，x2+4x+3），若∠AFC=90°，那么点F在y轴左侧；
①当点F在x轴下方时，过点F作FG⊥x轴于G，FH⊥y轴于H，如图①；
OG=FH=-x，FG=OH=-（x2+4x+3），
AG=OA-OG=3-（-x）=3+x，CH=OC+OH=3-（x2+4x+3）=-（x2+4x）；
∵∠FAC+∠ACF=90°，即∠CAG+∠FAG+∠ACF=90°，又∠CAG=45°，
∴∠FAG+∠ACF=45°；
∵∠ACO=∠ACF+∠FCH=45°，
∴∠FAG=∠FCH；
又∵∠AGF=∠CHF，
∴△AFG∽△CFH，得：
=
，即
=
，
解得：x1=
、x2=
（舍）；
则F（
，
）；
②当点F在x轴上方时，如图②；
同①求得 F（
，
）．
综上，点F的坐标为：（
，
）或（
，
）．
抛物线的顶点P的横坐标为-2，所以对称轴x=-2，则 B（-1，0）；
将点A、B、C的坐标代入抛物线的解析式中，得：
|
解得
|
故抛物线的解析式：y=x2+4x+3．
（2）由（1）的抛物线解析式知：y=x2+4x+3=（x+2）2-1，则顶点P（-2，-1）；
已知A（-3，0）、C（0，3），B（-1，0）、P（-2，-1）知：∠CAB=∠PBA=45°，AB=2、AC=3
| 2 |
| 2 |
①当∠ABC=∠BPD1时，△ABC∽△BPD1，得：
| BP |
| AB |
| BD1 |
| AC |
| ||
| 2 |
| BD1 | ||
3
|
则D1（-4，0），则 PD1=
| 5 |
故△PBD外接圆半径 r1=
| PD1 |
| 2sin∠PBD |
| ||
| 2•sin45° |
| ||||
2•
|
| ||
| 2 |
②当∠ABC=∠BD2P时，△ABC∽△BD2P，得：
| BP |
| AC |
| BD2 |
| AB |
| ||
3
|
| BD2 |
| 2 |
| 2 |
| 3 |
则D2（-
| 5 |
| 3 |
| ||
| 3 |
故△PBD外接圆半径 r2=
| PD2 |
| 2sin∠PBD |
| ||||
| 2•sin45° |
| ||||
2•
|
| ||
| 3 |
综上，有两组解分别是：①P（-2，-1），D1（-4，0），r1=
| ||
| 2 |
| 5 |
| 3 |
| ||
| 3 |
（3）若∠AEB为直角，那么点E在以AB为直径的⊙Q上，那么点E为直线l与⊙Q的交点（如右图）；取与直线l平行，且与⊙Q相切的直线l′、l″，如右图，设切点分别为M、N；
∵直线l∥直线l′∥直线l″，且它们的斜率k=1，
∴∠MKQ=∠NQL=45°．
Rt△KMQ中，QM=
| 1 |
| 2 |
| 2 |
同理可得 QL=
| 2 |
∴K（-2-
| 2 |
| 2 |
若直线l与⊙Q始终有两个交点，那么直线l必在直线l′、l″之间，由于直线l与x轴交点为（-t，0），有：
-2-
| 2 |
| 2 |
| 2 |
| 2 |
而∠AEB是直角，那么点A与点E以及点B与点E都不重合，即直线l不经过点A、B，所以，-t≠-1，且-t≠-3；
综上，t的取值范围：2-
| 2 |
| 2 |
（4）设点F（x，x2+4x+3），若∠AFC=90°，那么点F在y轴左侧；①当点F在x轴下方时，过点F作FG⊥x轴于G，FH⊥y轴于H，如图①；
OG=FH=-x，FG=OH=-（x2+4x+3），
AG=OA-OG=3-（-x）=3+x，CH=OC+OH=3-（x2+4x+3）=-（x2+4x）；
∵∠FAC+∠ACF=90°，即∠CAG+∠FAG+∠ACF=90°，又∠CAG=45°，
∴∠FAG+∠ACF=45°；
∵∠ACO=∠ACF+∠FCH=45°，
∴∠FAG=∠FCH；
又∵∠AGF=∠CHF，
∴△AFG∽△CFH，得：
| AG |
| CH |
| FG |
| FH |
| x+3 |
| -x(x+4) |
| -(x+1)(x+3) |
| -x |
解得：x1=
-5+
| ||
| 2 |
-5-
| ||
| 2 |
则F（
-5+
| ||
| 2 |
1-
| ||
| 2 |
②当点F在x轴上方时，如图②；
同①求得 F（
-5-
| ||
| 2 |
1+
| ||
| 2 |
综上，点F的坐标为：（
-5+
| ||
| 2 |
1-
| ||
| 2 |
-5-
| ||
| 2 |
1+
| ||
| 2 |
点评：此题考查了难度较大的函数与几何的综合题，主要涉及了：函数解析式的确定、三角形外接圆半径的求法、圆周角、直线与圆的位置关系以及相似三角形的判定和性质等重点知识；第三题中，由直角联想到圆是打开思路的关键；第二、四小题涉及到多种情况，应通过图形将各种情况分别列出进行分类讨论，以免出现漏解的情况．
练习册系列答案
相关题目
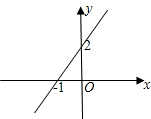如图，该直线是某个一次函数的图象，则此函数的解析式为
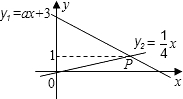如图，两直线y1=ax+3与y2=