题目内容
已知抛物线y=ax2+bx+c经过点A（-1，0），且经过直线y=x-3与x轴的交点B及与y轴的交点C．
（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．
解：（1）∵直线y=x-3与x轴的交点B及与y轴的交点C．
∴B（3，0），C（0，-3）．
设抛物线的解析式为y=a（x+1）（x-3），则有：
a（0+1）（0-3）=-3，
∴a=1，
∴y=x2-2x-3．
（2）由（1）知：y=x2-2x-3=（x-1）2-4，
因此顶点坐标为（1，-4）．
分析：（1）先根据直线y=x-3求出B、C的坐标，然后将A、B、C的坐标代入抛物线中即可求得抛物线的解析式．
（2）根据（1）的抛物线的解析式用配方或公式法均可求出顶点坐标．
点评：本题考查了待定系数法求二次函数的解析式、二次函数的性质．在设二次函数的解析式时，要根据不同的已知条件来设其解析式方程．
∴B（3，0），C（0，-3）．
设抛物线的解析式为y=a（x+1）（x-3），则有：
a（0+1）（0-3）=-3，
∴a=1，
∴y=x2-2x-3．
（2）由（1）知：y=x2-2x-3=（x-1）2-4，
因此顶点坐标为（1，-4）．
分析：（1）先根据直线y=x-3求出B、C的坐标，然后将A、B、C的坐标代入抛物线中即可求得抛物线的解析式．
（2）根据（1）的抛物线的解析式用配方或公式法均可求出顶点坐标．
点评：本题考查了待定系数法求二次函数的解析式、二次函数的性质．在设二次函数的解析式时，要根据不同的已知条件来设其解析式方程．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
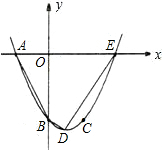与x轴的另一个交点为E．
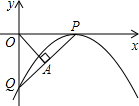如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=