题目内容
【题目】如图所示,在长方形ABCD中,AB=CD=8cm,AD=BC=6cm,点E是DC边上一点,且CE=1cm,动点P从A点出发,沿折线A-D-E以acm/s的速度向终点E运动,运动时间为t秒,已知a是方程
的解.
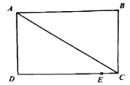
(1)求a的值；
(2)点P在运动过程中,请用t的式子表示△APC的面积；
(3)在点P运动的同时,有一动点Q从C点出发,沿折线C-D-A以1cm/s的速度向终点A运动,运动过程中,一个点停止运动时另一个点继续向终点运动,当△APC和△AQC的面积相差6平方厘米时,求t的值.
【答案】（1）a=2;
（2）S△APC=8t（0＜t≤3），S△APC=42-6t（3＜t≤6.5）（3）t=
，4，
时，△APC和△AQC的面积相差6平方厘米.
【解析】
（1）解出含a的方程即可；
（2）分P点在AD上和在DE上分别求解；
（3）分Q在CD上，Q在AD上求出△AQC的面积，再进行比较计算.
（1）解方程
15-6a+2=5
-6a=-12
a=2,
∴a=2;
（2）当P点在AD上，0＜t≤3时，AP=2t，
S△APC=
AP×CD=×2t×8=8t（0＜t≤3）
当P在DE上，3＜t≤6.5时，DP=2t-6，PC=CD-DP=14-2t，
S△APC=PC×AD=×（14-2t）×6=42-6t（3＜t≤6.5）
（3）当Q点在CD上，0＜t≤8时，CQ=t，
S△APC=CQ×AD=×t×6=3t（0＜t≤8）
当P在AD上，8＜t≤14时，DQ=t-8，AQ=AD-DQ=14-t，
S△APC=AQ×CD=×（14-t）×8=56-4t（8＜t≤14）
∵当△APC和△AQC的面积相差6平方厘米
∴①8t-3t=6,解得t=（符合题意）
②42-6t-3t=6，解得t=4（符合题意）
③当P点到达终点时，t=6.5，S△APC=3，
令3t-3=6，t=3（不符合题意），令56-4t-3=6，解得t=（符合题意）
综上：t=，4，时，△APC和△AQC的面积相差6平方厘米.
