题目内容
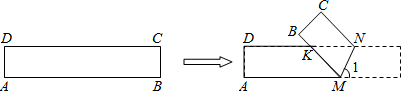
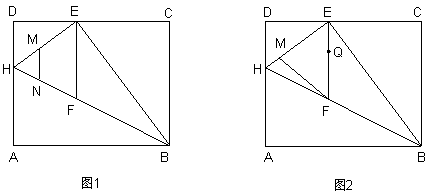
如图,ABCD是一张矩形纸片,AB=20cm,BC=16cm,在AD边上取一点H,将纸片沿BH翻折,使点A恰好落在DC边上的点E处,过点E作EF∥AD交HB于点F
(1)求EF的长;
(2)若点M自点H沿HE方向以1cm/s的速度向E点运动(不与H,E重合),过点M作MN∥EF交HB于点N,如图2,将△HMN沿MN对折,点H的对应点为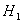 ,若△
,若△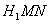 与四边形
与四边形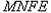 重叠部分的面积为
重叠部分的面积为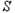 ,点M运动的时间为
,点M运动的时间为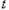 秒,问当
秒,问当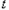 为何值时,
为何值时,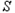 有最大值,最大值是多少。
有最大值,最大值是多少。
(3)当(2)问,点M自点H沿HE方向以1cm/s的速度向E点运动的同时点Q从点E出发,以2cm/s的速度运动,当点Q到达F点时M,Q停止运动,连接MF,是否存在某一时刻t,使点Q在线段MF的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
(1)求EF的长;
(2)若点M自点H沿HE方向以1cm/s的速度向E点运动(不与H,E重合),过点M作MN∥EF交HB于点N,如图2,将△HMN沿MN对折,点H的对应点为
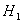 ,若△
,若△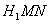 与四边形
与四边形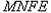 重叠部分的面积为
重叠部分的面积为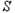 ,点M运动的时间为
,点M运动的时间为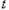 秒,问当
秒,问当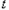 为何值时,
为何值时,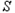 有最大值,最大值是多少。
有最大值,最大值是多少。(3)当(2)问,点M自点H沿HE方向以1cm/s的速度向E点运动的同时点Q从点E出发,以2cm/s的速度运动,当点Q到达F点时M,Q停止运动,连接MF,是否存在某一时刻t,使点Q在线段MF的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.
解:(1)10
(2)当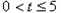
 当t=5时,S最大=10
当t=5时,S最大=10
当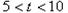 S=
S= 当 t=5时,S最大=10
当 t=5时,S最大=10
(3)假设存在某一时刻t,使点Q在线段MF的垂直平分线上,则MQ=QF,
过Q作QG⊥HE,交HE于G,HK⊥EF,
所以△QGE∽△HKE
∴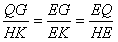 ,HK=8,EK=6
,HK=8,EK=6
 ,QG=
,QG= ,
,
EG=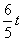 ,MG=
,MG=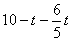
在Rt△MQG中,
FQ=10-2t
∴ :
:
 (舍去)
(舍去)
(2)当
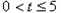
 当t=5时,S最大=10
当t=5时,S最大=10当
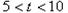 S=
S= 当 t=5时,S最大=10
当 t=5时,S最大=10 (3)假设存在某一时刻t,使点Q在线段MF的垂直平分线上,则MQ=QF,
过Q作QG⊥HE,交HE于G,HK⊥EF,
所以△QGE∽△HKE
∴
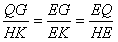 ,HK=8,EK=6
,HK=8,EK=6  ,QG=
,QG= ,
,EG=
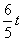 ,MG=
,MG=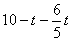
在Rt△MQG中,

FQ=10-2t
∴
 :
: (舍去)
(舍去)
练习册系列答案
相关题目
 B、
B、 C、
C、 D、
D、
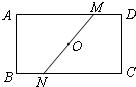
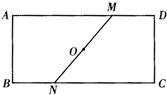 20、如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于M,交BC于N.
20、如图,ABCD是一张矩形纸片,点O为矩形对角线的交点,直线MN经过点O交AD于M,交BC于N.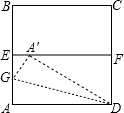 如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=
如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG= 15、如图,ABCD是一张矩形纸片,沿过点D的折痕将A角翻折,使得点A落在BC上,折痕交AB于点E,若BC=2AB,则∠A′EB=
15、如图,ABCD是一张矩形纸片,沿过点D的折痕将A角翻折,使得点A落在BC上,折痕交AB于点E,若BC=2AB,则∠A′EB=