题目内容
【题目】如图，已知正方形ABCD中，以BF为底向正方形外侧作等腰直角三角形BEF，连接DF，取DF的中点G，连接EG，CG.
(1)如图1，当点A与点F重合时，猜想EG与CG的数量关系为 ，EG与CG的位置关系为 ，请证明你的结论.
(2)如图2，当点F在AB上（不与点A重合）时，（1）中结论是否仍然成立？请说明理由；如图3，点F在AB的左侧时，（1）中的结论是否仍然成立？直接做出判断，不必说明理由.
(3)在图2中，若BC=4，BF=3，连接EC，求
的面积.
【答案】（1）EG=CG，EG⊥CG；（2）当点F在AB上（不与点A重合）时，（1）中结论仍然成立，理由见解析，点F在AB的左侧时，（1）中的结论仍然成立；（3）S△CEG=
.
【解析】
（1）过E作EM⊥AD交AD的延长线于M，证明△AME是等腰直角三角形，得出AM=EM=
AE=
AB，证出DG=AG=AD=AM=EM，得出GM=CD，证明△GEM≌△CGD（SAS），得出EG=CG，∠EGM=∠GCD，证出∠CGE=180°-90°=90°，即可得出EG⊥CG；
（2）延长EG至H，使HG=EG，连接DH、CH、CE，证明△EFG≌△HDG（SAS），得出EF=HD，∠EFG=∠HDG，证明△CBE≌△CDH（SAS），得出CE=CH，∠BCE=∠DCH，得出∠ECH=∠BCD=90°，证明△ECH是等腰直角三角形，得出CG=EH=EG，EG⊥CG；延长EG至H，使HG=EG，连接DH、CH、CE，同理可证CG=EH=EG，EG⊥CG；
（3）作EM垂直于CB的延长线与M，先求出BM，EM的值，即可根据勾股定理求出CE的长度，从而求出CG的长，即可求出面积.
解：（1）EG=CG，EG⊥CG；理由如下：
过E作EM⊥AD交AD的延长线于M，如图1所示：
则∠M=90°，
∵四边形ABCD是正方形，
∴AB=AD=CD，∠BAD=∠D=90°，
∴∠BAM=90°，
∵△BEF是等腰直角三角形，
∴∠BAE=45°，AE=AB，
∴∠MAE=45°，
∴△AME是等腰直角三角形，
∴AM=EM=AE=AB，
∵G是DF的中点，
∴DG=AG=AD=AM=EM，
∴GM=CD，
在△GEM和△CGD中，
，
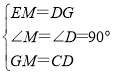∴△GEM≌△CGD（SAS），
∴EG=CG，∠EGM=∠GCD，
∵∠GCD+∠DGC=90°，
∴∠EGM+∠DGC=90°，
∴∠CGE=180°-90°=90°，
∴EG⊥CG；
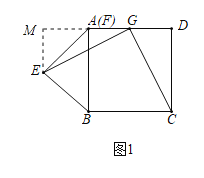
（2）当点F在AB上（不与点A重合）时，（1）中的结论仍然成立，理由如下：
延长EG至H，使HG=EG，连接DH、CH、CE，如图2所示：
∵G是DF的中点，
∴FG=DG，
在△EFG和△HDG中，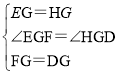
，
∴△EFG≌△HDG（SAS），
∴EF=HD，∠EFG=∠HDG，
∵△BEF是等腰直角三角形，
∴EF=BE，∠BFE=∠FBE=45°，
∴BE=DH，
∵四边形ABCD是正方形，
∴AB∥CD，∠ABC=∠BCD=90°，BC=CD，
∴∠AFD=∠CDG，
∴∠AFE=∠CDH=135°，
∵∠CBE=90°+45°=135°，
∴∠CBE=∠CDH，
在△CBE和△CDH中，
，
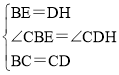∴△CBE≌△CDH（SAS），
∴CE=CH，∠BCE=∠DCH，
∴∠ECH=∠BCD=90°，
∴△ECH是等腰直角三角形，
∵EG=HG，
∴CG=EH=EG，EG⊥CG；
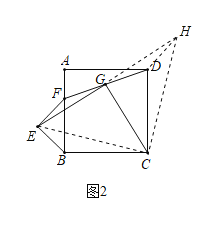
点F在AB的左侧时，（1）中的结论仍然成立，理由如下：
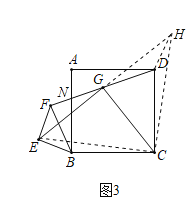
延长EG至H，使HG=EG，连接DH、CH、CE，如图3所示：
∵G是DF的中点，
∴FG=DG，
在△EFG和△HDG中，
，
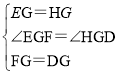∴△EFG≌△HDG（SAS），
∴EF=HD，∠EFG=∠HDG，
∵△BEF是等腰直角三角形，
∴EF=BE，∠BEF=90°，
∴BE=DH，
∵四边形ABCD是正方形，
∴AB∥CD，∠ABC=∠BCD=90°，BC=CD，
∴∠BNF=∠CDG，
∵∠EFG+∠BNF+∠BEF+∠ABE=∠HDG+∠CDG+∠CDH=360°，
∴∠BEF+∠ABE=∠CDH，
∴∠ABC+∠ABE=∠CDH，即∠CBE=∠CDH，
在△CBE和△CDH中，
，
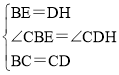∴△CBE≌△CDH（SAS），
∴CE=CH，∠BCE=∠DCH，
∴∠ECH=∠BCD=90°，
∴△ECH是等腰直角三角形，
∵EG=HG，
∴CG=EH=EG，EG⊥CG；
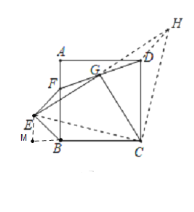
（3）如下图所示：作EM垂直于CB的延长线与M，
∵△BEF为等腰直角三角形，BF=3，
∴BE=
，∠ABE=45°，
∵EM⊥BM，AB⊥CM，
∴∠EBM=45°，
∴△EMB为等腰直角三角形，
∴EM=BM=
，
∵BC=4，
∴CM=
，
∴CE=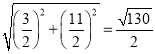
，
由（2）知，△GEC为等腰直角三角形，
∴CG=EG=
，
∴S△CEG=
.
