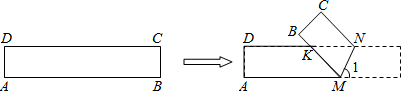
��Ŀ����
��ͼ��ABCD��һ�ž���ֽƬ��AB=20cm��BC=16cm����AD����ȡһ��H����ֽƬ��BH���ۣ�ʹ��Aǡ������DC���ϵĵ�E��������E��EF��AD��HB�ڵ�F��
��1����EF�ij���
��2������M�Ե�H��HE������1cm/s���ٶ���E���˶�������H��E�غϣ�������M��MN��EF��HB�ڵ�N����ͼ2������HMN��MN���ۣ���H�Ķ�Ӧ��ΪH1������H1MN���ı���MNFE�ص����ֵ����ΪS����M�˶���ʱ��Ϊt�룬�ʵ�tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3������2���ʣ���M�Ե�H��HE������1cm/s���ٶ���E���˶���ͬʱ��Q�ӵ�E��������2cm/s���ٶ��˶�������Q����F��ʱM��Qֹͣ�˶�������MF���Ƿ����ijһʱ��t��ʹ��Q���߶�MF�Ĵ�ֱƽ�����ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�

��1����EF�ij���
��2������M�Ե�H��HE������1cm/s���ٶ���E���˶�������H��E�غϣ�������M��MN��EF��HB�ڵ�N����ͼ2������HMN��MN���ۣ���H�Ķ�Ӧ��ΪH1������H1MN���ı���MNFE�ص����ֵ����ΪS����M�˶���ʱ��Ϊt�룬�ʵ�tΪ��ֵʱ��S�����ֵ�����ֵ�Ƕ��٣�
��3������2���ʣ���M�Ե�H��HE������1cm/s���ٶ���E���˶���ͬʱ��Q�ӵ�E��������2cm/s���ٶ��˶�������Q����F��ʱM��Qֹͣ�˶�������MF���Ƿ����ijһʱ��t��ʹ��Q���߶�MF�Ĵ�ֱƽ�����ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�

��������1�������۵������ʡ����ɶ�����ֱ�ǡ�BCE�����EC=12cm�������������ε��ж���֪��ECB�ס�HDE�����Ը��ݡ����������εĶ�Ӧ�߳ɱ��������EH=AH=10cm��Ȼ�����á�ABH�����к����Ķ������FG=6cm���������߶�EF�ij��ȣ�
��2�����������ε������ʽ���S��t�ĺ�����ϵʽ�����ݺ�����ϵʽ������ֵ��
��3����Q��QG��HE��HE��G��HK��EF���������������Σ���QGE�ס�HKE�������ɡ����������εĶ�Ӧ�߳ɱ������������г�����t��һԪ���η��̣�ͨ���ⷽ������t��ֵ��
��2�����������ε������ʽ���S��t�ĺ�����ϵʽ�����ݺ�����ϵʽ������ֵ��
��3����Q��QG��HE��HE��G��HK��EF���������������Σ���QGE�ס�HKE�������ɡ����������εĶ�Ӧ�߳ɱ������������г�����t��һԪ���η��̣�ͨ���ⷽ������t��ֵ��
���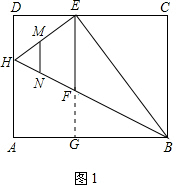 �⣺��1���۵�������֪����A=��HEB=90�㣬AH=EH��AB=EB��
�⣺��1���۵�������֪����A=��HEB=90�㣬AH=EH��AB=EB��
����Rt��ECB��EB=20cm��BC=16cm��
����ݹ��ɶ���֪EC=
=
=12��cm����
�ߡ�EBC=��DEH��ͬ�ǵ������ȣ�����C=��D=90�㣬
���ECB�ס�HDE��
��
=
��
��
=
����
=
��
���EH=AH=10cm��
��ͼ1���ӳ�ֱ��EF��AB����ΪG��
���ı���ABCD�Ǿ��Σ�
��EC��GB����C=90�㣬
���ı���ECBGΪ���Σ�
��EC=BG=12cm��EG=BC=16cm��
��
=
����
=
��
��FG=6cm��
��EF=EG-FG=16-6=10��cm����
��2�����ݶ��۵�����֪����HMN�ա�H1MN����S��HMN=S��H1MN��
�ɣ�1��֪��DE=8cm��EH=EF=10cm��
��AD��DE��EF��AD��
��DE��EF��
��S��HEF=
EF•DE=
��10��8=40��cm2����
��MN��EF��
���HMN�ס�HEF��
��
=(
)2����
=(
)2��
��S��HMN=
t2����0��t��10����
����ͼ2��ʾ����0��t��5ʱ��S=S��HMN=
t2����
��t=5ʱ��S���=
��25=10��cm2����
�ڵ�5��t��10ʱ����ͼ3��ʾ������HH1����HH1��MN��HH1��EF��
���ݶ��۵�����֪��HK=H1K��
�ߡ�HMN�ס�HEF��
��
=
����
=
��
��
=
��
��
=
��
��MN��EF����MN��GI��
���H1GI�ס�H1MN��
��
=
=��
��2=��
��2��
��S��H1GI=
��t-5��2��
��S=S��HMN-S��H1GI=-
t2+16t-40=-
��t-
��2+
��
�൱t=
ʱ��S���=
��
������������t=
ʱ��S���=
��cm2����

��3���������ijһʱ��t��ʹ��Q���߶�MF�Ĵ�ֱƽ�����ϣ���MQ=QF��
��ͼ4����Q��QG��HE����HE��G��HK��EF�����QGE�ס�HKE��
��
=
=
��
��HK=8cm��EK=6cm��
��
=
=
��
��QG=
t��EG=
t��MG=10-t-
t=10-
t��
��Rt��MQG��MQ2=��
t��2+��10-
t��2=
t2-44t+100��FQ=10-2t��
��
t2-44t+100=100-40t+4t2����ã�t1=
��t2=0����ȥ����
 �⣺��1���۵�������֪����A=��HEB=90�㣬AH=EH��AB=EB��
�⣺��1���۵�������֪����A=��HEB=90�㣬AH=EH��AB=EB������Rt��ECB�У�EB=20cm��BC=16cm��
����ݹ��ɶ���֪EC=
| EB2-BC2 |
| 202-162 |
�ߡ�EBC=��DEH��ͬ�ǵ������ȣ�����C=��D=90�㣬
���ECB�ס�HDE��
��
| BC |
| EB |
| DE |
| EH |
��
| BC |
| AB |
| DC-EC |
| EH |
| 16 |
| 20 |
| 8 |
| EH |
���EH=AH=10cm��
��ͼ1���ӳ�ֱ��EF��AB����ΪG��
���ı���ABCD�Ǿ��Σ�
��EC��GB����C=90�㣬
���ı���ECBGΪ���Σ�
��EC=BG=12cm��EG=BC=16cm��
��
| AH |
| AB |
| FG |
| BG |
| 10 |
| 20 |
| FG |
| 12 |
��FG=6cm��
��EF=EG-FG=16-6=10��cm����
��2�����ݶ��۵�����֪����HMN�ա�H1MN����S��HMN=S��H1MN��
�ɣ�1��֪��DE=8cm��EH=EF=10cm��
��AD��DE��EF��AD��
��DE��EF��
��S��HEF=
| 1 |
| 2 |
| 1 |
| 2 |

��MN��EF��
���HMN�ס�HEF��
��
| S��HMN |
| S��HEF |
| HM |
| HE |
| S��HMN |
| 40 |
| t |
| 10 |
��S��HMN=
| 2 |
| 5 |
����ͼ2��ʾ����0��t��5ʱ��S=S��HMN=
| 2 |
| 5 |
��t=5ʱ��S���=
| 2 |
| 5 |
�ڵ�5��t��10ʱ����ͼ3��ʾ������HH1����HH1��MN��HH1��EF��
���ݶ��۵�����֪��HK=H1K��
�ߡ�HMN�ס�HEF��

��
| HK |
| HJ |
| HM |
| HE |
| HK |
| HJ |
| t |
| 10 |
��
| HK |
| KJ |
| t |
| 10-t |
��
| H1K |
| H1J |
| t |
| 2t-10 |
��MN��EF����MN��GI��
���H1GI�ס�H1MN��
��
| S��HMN |
| S��H1GI |
| S��H1MN |
| S��H1GI |
| H1K |
| H1J |
| t |
| 2t-10 |
��S��H1GI=
| 8 |
| 5 |
��S=S��HMN-S��H1GI=-
| 6 |
| 5 |
| 6 |
| 5 |
| 20 |
| 3 |
| 40 |
| 3 |
�൱t=
| 20 |
| 3 |
| 40 |
| 3 |
������������t=
| 20 |
| 3 |
| 40 |
| 3 |

��3���������ijһʱ��t��ʹ��Q���߶�MF�Ĵ�ֱƽ�����ϣ���MQ=QF��
��ͼ4����Q��QG��HE����HE��G��HK��EF�����QGE�ס�HKE��
��
| QG |
| HK |
| EG |
| EH |
| EQ |
| HE |
��HK=8cm��EK=6cm��
��
| QG |
| 8 |
| EG |
| 6 |
| 2t |
| 10 |
��QG=
| 8 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 11 |
| 5 |
��Rt��MQG��MQ2=��
| 8 |
| 5 |
| 11 |
| 5 |
| 37 |
| 5 |
��
| 37 |
| 5 |
| 20 |
| 17 |
���������⿼���������ۺ��⣮ע�����и����ߵ����������⣬���2��ʱ��Ҫ�������ۣ��Է�©�⣮

��ϰ��ϵ�д�
�����Ŀ
 B��
B�� C��
C�� D��
D��
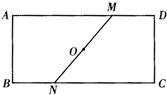 20����ͼ��ABCD��һ�ž���ֽƬ����OΪ���ζԽ��ߵĽ��㣬ֱ��MN������O��AD��M����BC��N��
20����ͼ��ABCD��һ�ž���ֽƬ����OΪ���ζԽ��ߵĽ��㣬ֱ��MN������O��AD��M����BC��N��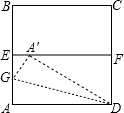 ��ͼ��ABCD��һ�ű߳�Ϊ4cm��������ֽƬ��E��F�ֱ�ΪAB��CD���е㣬�ع���D���ۺ۽�A �Ƿ��ۣ�ʹ�õ�A����EF�ϵĵ�A�䴦���ۺ۽�AE�ڵ�G����EG=
��ͼ��ABCD��һ�ű߳�Ϊ4cm��������ֽƬ��E��F�ֱ�ΪAB��CD���е㣬�ع���D���ۺ۽�A �Ƿ��ۣ�ʹ�õ�A����EF�ϵĵ�A�䴦���ۺ۽�AE�ڵ�G����EG=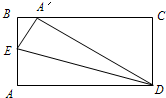 15����ͼ��ABCD��һ�ž���ֽƬ���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ��ۺ۽�AB�ڵ�E����BC=2AB�����A��EB=
15����ͼ��ABCD��һ�ž���ֽƬ���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ��ۺ۽�AB�ڵ�E����BC=2AB�����A��EB=