题目内容
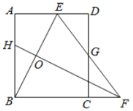
【题目】如图，在ABCD中，BC＝6cm，点E从点D出发沿DA边运动到点A，点F从点B出发沿BC边向点C运动，点E的运动速度为2cm/s，点F的运动速度为lcm/s，它们同时出发，设运动的时间为t秒，当t为何值时，EF∥AB．
【答案】t＝2
【解析】
当运动时间为t秒时，BF＝tcm，AE＝（6﹣2t）cm，由EF∥AB，BF∥AE可得出四边形ABFE为平行四边形，利用平行四边形的性质可得出关于t的一元一次方程，解之即可得出结论．
解：当运动时间为t秒时，BF＝tcm，AE＝（6﹣2t）cm，
∵EF∥AB，BF∥AE，
∴四边形ABFE为平行四边形，
∴BF＝AE，即t＝6﹣2t，
解得：t＝2．
答：当t＝2秒时，EF∥AB．
练习册系列答案
相关题目
