题目内容
【题目】如图,直角坐标系中,△ABC的三个顶点的坐标分别为(2,1),(﹣1,3),(﹣3,2).
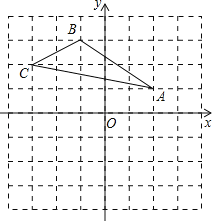
(1)在图中作出△ABC关于x轴对称的△A′B′C′,并写出点A′的坐标为 ,点B的坐标为 ,点C′的坐标为 ;
(2)求△ABC的面积;
(3)若点P(a,a﹣2)与点Q关于y轴对称,若PQ=8,求点P的坐标.
【答案】(1)见解析,A′(2,﹣1),B′(﹣1,﹣3),C′(﹣3,﹣2);(2)3.5;(3)点P的坐标为(4,2)或(﹣4,﹣6).
【解析】
(1)根据关于x轴对称的点的坐标特征,横坐标相反,纵坐标相同即可求得对应点的坐标.
(2)根据割补法将求△ABC的面积问题转化为求其它图形的面积和或面积差问题.
(3)根据关于y轴对称的点的坐标特征,横坐标相反,纵坐标相同将Q点的坐标用a表示出来,然后列出线段PQ的长的关系式,求解即可.
解:
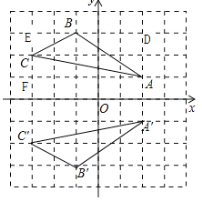
(1)如图,△A′B′C′为所作;
A′(2,﹣1),B′(﹣1,﹣3),C′(﹣3,﹣2);
(2)![]()
=![]()
=3.5
(3)∵点P(a,a﹣2)与点Q关于y轴对称,
∴Q(﹣a,a﹣2),
∵PQ=8,
∴|a﹣(﹣a)|=8,
解得a=4或a=﹣4,
∴点P的坐标为(4,2)或(﹣4,﹣6).

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目